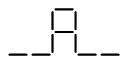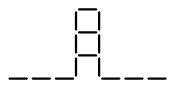9.2.1A Functions & Other Relations
Understand the definition of a function. Use functional notation and evaluate a function at a given point in its domain.
For example: If f(x)=$\frac{1}{x^{2}-3}$, find f(-4).
Distinguish between functions and other relations defined symbolically, graphically or in tabular form.
Find the domain of a function defined symbolically, graphically or in a real-world context.
For example: The formula f(x) = πx2 can represent a function whose domain is all real numbers, but in the context of the area of a circle, the domain would be restricted to positive x.
Obtain information and draw conclusions from graphs of functions and other relations.
For example: If a graph shows the relationship between the elapsed flight time of a golf ball at a given moment and its height at that same moment, identify the time interval during which the ball is at least 100 feet above the ground.
Overview
Standard 9.2.1 Essential Understandings
The concept of function is one of the most important ideas in school mathematics. Functions are a way to study the relationship among two or more variables and organize the world. The definition of a mathematical function developed over a thousand years. The beginning focus was on the covariation of two variables. Studying how two variables change together constitutes much of the middle and secondary curriculum. As the definition of function evolved the "exactly one" feature of the function gained importance. This feature is highlighted when students are asked to distinguish between relations that are functions and those that are not.
In elementary school, students begin to study functions by finding rules for various patterns. The rule for determining the number of toothpicks in a figure is a function relating the figure number (independent variable) with the number of toothpicks in that figure (dependent variable).
|
|
|
|
|
|
figure number |
1 |
2 |
3 |
|
number of toothpicks in figure |
5 |
10 |
15 |
Students explain that the number of toothpicks is the figure number multiplied by five.
Thinking of functions as rules that generalize patterns is developed further in middle school where students learn that a proportional relationship between two variables exists if the rule relating the variables is written as y = m • x. They also can see this relationship graphically as a line passing through the origin. At the end of middle school, students are able to distinguish between linear functions and functions that are not linear by inspecting the function represented by a table, graph, equation, or a real-world situation.
Students at the secondary level use their knowledge of how linear functions change and relate it to how exponential and quadratic functions change. Among the functions that students study in high school is the rate of change as shown in tables, graphs, and equations, one of the most important features that distinguish the different types. Parts of the curves of quadratic and exponential functions can appear to be similar on a graph, but the differences in the rates of change show that no quadratic or exponential will ever match at more than just a few discrete points. Quadratic functions and exponential functions can both increase at an increasing rate but these patterns of change are quite different.
Functions are tools that people use to model relationships between two variables. In middle school students use linear functions to model real-world situations. The function W(t) = 15t + 7 could represent to weights of baby girls when they are t months old. Students learn how special features of the function relate to the real-world situation. The y-intercept represents the weight of the baby girl at birth, while the slope represents the number of pounds that the baby gains each month. In addition, the domain of the function is determined by the constraints of the real-world setting. Theoretically, the domain of any linear function could be the set of real numbers, but practically the function does not really make sense for values of ![]() that are less than 0 months or larger than 6 months.
that are less than 0 months or larger than 6 months.
In high school students are expected to identify theoretical and practical domains for a variety of functions. In particular, students in secondary school will focus on the special features of quadratic, exponential, and reciprocals of linear functions. These special features provide insights into the real-world situation being modeled. The vertex of a quadratic function could be used to find the maximum or minimum value of the dependent variable while the asymptote of an exponential function could be used to describe the long-term behavior of a situation. Students in high school need to make connections among equations, graphs, tables, and real-world situations of a variety of functions at the high school level. Each representation provides insights into how student make sense of these functions.
Once students are able to identify important features of a variety of functions then they move to seeing how functions can be transformed. Initially students see graphs of functions as a collection of individual points and then move to seeing the graph as an object itself made up of an infinite number of points. Students initially graph functions like f(x) = (x + 3)2 and g(x) = x + 2 by calculating points to put in a table, then using these points to create a graph. The more points they create the better the graph looks. They then learn to identify the intercepts and, if applicable, the vertex. This process reinforces the notion of a graph as a collection of a finite set of points. Eventually students are asked to combine functions to create new functions (i.e. find h(x) = f(x) + g(x) or k(x) = g(f(x))). These operations and compositions of functions force students to think of the functions themselves as objects. Students need to view the graphs of functions as objects when they are asked to explain how the graph of a function f(x) compares with the graph of the function m(x) where m(x) = f(x) + 5 or the graph of p(x) where p(x) = f(x + 7). Students at the high school level need to see that a vertical translation is the sum of the original function, and a constant function and a horizontal translation is a composition of the original function with a linear function that has a slope of one; i.e., the graph of the function w(x - 11) is a horizontal translation of the graph of w(x) 11 units to the right.
In high school students gain experience distinguishing among different types of functions and sort them into families. Students learn to identify key features of each type using graphs, tables, equations, and real-world situations. The students then begin to perform operations using the functions themselves as inputs. The results of these operations allow students to create new types of functions that can be used to solve new problems.
All Standard Benchmarks
9.2.1.1
Understand the definition of a function. Use functional notation and evaluate a function at a given point in its domain.
9.2.1.2
Distinguish between functions and other relations defined symbolically, graphically or in tabular form.
9.2.1.3
Find the domain of a function defined symbolically, graphically or in a real-world context.
9.2.1.4
Obtain information and draw conclusions from graphs of functions and other relations.
9.2.1.5
Identify the vertex, line of symmetry and intercepts of the parabola corresponding to a quadratic function, using symbolic and graphical methods, when the function is expressed in the form f(x) = ax2 + bx + c, in the form f(x) = a( x - h)2 + k , or in factored form.
9.2.1.6
Identify intercepts, zeros, maxima, minima and intervals of increase and decrease from the graph of a function.
9.2.1.7
Understand the concept of an asymptote and identify asymptotes for exponential functions and reciprocals of linear functions, using symbolic and graphical methods.
9.2.1.8
Make qualitative statements about the rate of change of a function, based on its graph or table of values.
9.2.1.9
Determine how translations affect the symbolic and graphical forms of a function. Know how to use graphing technology to examine translations.
Benchmark Group A - Functions and Other Relations
9.2.1.1
Understand the definition of a function. Use functional notation and evaluate a function at a given point in its domain.
9.2.1.2
Distinguish between functions and other relations defined symbolically, graphically or in tabular form.
9.2.1.3
Find the domain of a function defined symbolically, graphically or in a real-world context.
9.2.1.4
Obtain information and draw conclusions from graphs of functions and other relations.
What students should know and be able to do [at a mastery level] related to these benchmarks.
- Students should know different notation conventions that represent functions (e.g., y = 12x, f(x) = -2x2 + 3x, an = 3n + 7, an = 2an-1 + 7) and be able to identify the independent variable as well as the dependent variable in these equations.
- Students should be able to evaluate the value of the dependent variable given the value of the independent variable (e.g., "Find f(3) if f(x) = -2x2 + 3x").
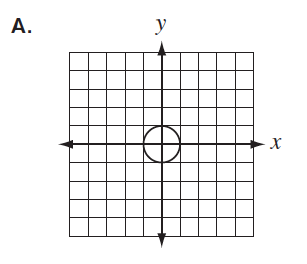
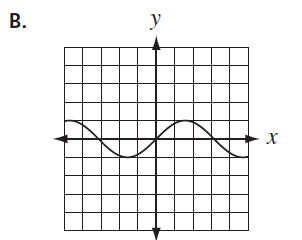
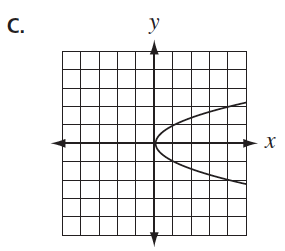
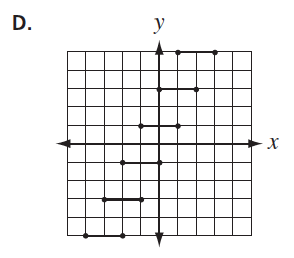
- Students should be able to use the definition of a function to distinguish examples of relations that are functions from relations that are not functions displayed symbolically, graphically, and in tabular form.
|
|
function |
not a function |
||||||||||||||||||||||||
|
symbol |
$f(x)=3^{x}+5$ |
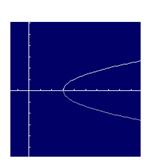
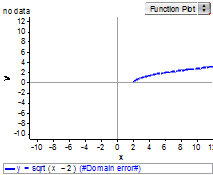
$g(x)=\pm\sqrt{x-3}$ |
||||||||||||||||||||||||
|
graph |
|
|
||||||||||||||||||||||||
|
table |
|
|
- Students should be able to determine the domain of a function defined symbolically, graphically, or within a real-world situation.
|
representation |
example |
domain |
|
symbolic |
$f(x)=\sqrt{x+3}$ |
The domain is all real numbers greater than or equal to -3. |
|
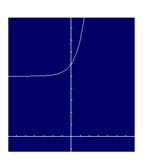
graphical |
|
The domain is all real numbers greater than or equal to 2. |
|
real-world situation |
A square piece of metal measuring 3ft by 3ft is cut into a box by cutting squares from each of the four corners. The volume of the box can be modeled by the function $V(x)=(3-2X)^{2}\times x$. |
In real world situations there is a practical domain and a theoretical domain. Theoretically the domain is the set of real numbers. Practically the domain is $0<x<1.5$. |
- Students should be able to use features of a graph to answer questions related to the context of the situation. Examples should include naked functions, context, and a relation that is not a function.
Work from previous grades that supports this new learning includes:
- Students entering grades 9-11 taking algebra should be able to distinguish between linear and non-linear functions displayed symbolically, graphically, in tabular form, and in real-world situations.
- Students can use function notation to represent relationships in which changing the input variable by some amount leads to a change in the output variable that is a constant times that amount. (e.g., "Given y = 3x - 7, how does the value of y change if the value of x increases by 5?")
- Students recognize that a function is linear if it can be expressed in the form f(x) = mx + b or if its graph is a straight line.
- Students should understand that an arithmetic sequence is a linear function that can be expressed in the form f(x) = mx + b, where x = 0, 1, 2, 3,...
- Students should further understand that a geometric sequence is a non-linear function that can be expressed in the form f(x) = a • bx where x = 0, 1, 2, 3,...
NCTM Standards: (those that apply to 9.2.1 are bolded)
(p.296, PSSM) Instructional programs from Pre-K through grade 12 should enable all students to:
1. Understand patterns, relations, and functions. In grades 9-12 all students should
- generalize patterns using explicitly defined and recursively defined functions;
- understand relations and functions and select, convert flexibly among, and use various representations for them;
- analyze functions of one variable by investigating rates of change, intercepts, zeros, asymptotes, and local and global behavior;
- understand and perform transformations such as arithmetically combining, composing, and inverting commonly used functions, using technology to perform such operations on more-complicated symbolic expressions;
- understand and compare the properties of classes of functions, including exponential, polynomial, rational, logarithmic, and periodic functions;
- interpret representations of functions of two variables.
2. Represent and analyze mathematical situations and structures using algebraic symbols. In grades 9-12 all students should
- understand the meaning of equivalent forms of expressions, equations, inequalities, and relations;
- write equivalent forms of equations, inequalities, and systems of equations and solve them with fluency - mentally or with paper and pencil in simple cases and using technology in all cases;
- use symbolic algebra to represent and explain mathematical relationships;
- use a variety of symbolic representations, including recursive and parametric equations, for functions and relations;
- judge the meaning, utility, and reasonableness of the results of symbol manipulations, including those carried out by technology.
3. Use mathematical models to represent and understand quantitative relationships. In grades 9-12 all students should
- identify essential quantitative relationships in a situation and determine the class or classes of functions that might model the relationships;
- use symbolic expressions, including iterative and recursive forms, to represent relationships arising from various contexts;
- draw reasonable conclusions about a situation being modeled.
4. Analyze change in various contexts. In grades 9-12 all students should
- approximate and interpret rates of change from graphical and numerical data.
Common Core State Standards (CCSM)
High School: Functions
F-IF.1. Understand that a function from one set (called the domain) to another set (called the range) assigns to each element of the domain exactly one element of the range. If f is a function and x is an element of its domain, then f(x) denotes the output of f corresponding to the input x. The graph of f is the graph of the equation y = f(x).
F-IF.2. Use function notation, evaluate functions for inputs in their domains, and interpret statements that use function notation in terms of a context.
F-IF.4. For a function that models a relationship between two quantities, interpret key features of graphs and tables in terms of the quantities, and sketch graphs showing key features given a verbal description of the relationship. Key features include: intercepts; intervals where the function is increasing, decreasing, positive, or negative; relative maximums and minimums; symmetries; end behavior; and periodicity.★
F-IF.5. Relate the domain of a function to its graph and, where applicable, to the quantitative relationship it describes. For example, if the function h(n) gives the number of person-hours it takes to assemble n engines in a factory, then the positive integers would be an appropriate domain for the function.★
F-IF.6. Calculate and interpret the average rate of change of a function (presented symbolically or as a table) over a specified interval. Estimate the rate of change from a graph.★
F-IF.7. Graph functions expressed symbolically and show key features of the graph, by hand in simple cases and using technology for more complicated cases.★
- Graph linear and quadratic functions and show intercepts, maxima, and minima.
- (+) Graph rational functions, identifying zeros and asymptotes when suitable factorizations are available, and showing end behavior.
- Graph exponential functions, showing intercepts and end behavior.
F-IF.8. Write a function defined by an expression in different but equivalent forms to reveal and explain different properties of the function.
- Use the process of factoring and completing the square in a quadratic function to show zeros, extreme values, and symmetry of the graph, and interpret these in terms of a context.
- Use the properties of exponents to interpret expressions for exponential functions. For example, identify percent rate of change in functions such as $y=(1.02)^{t}$, $y=(0.97)^{t}$, $y=(1.01)^{12t}$, $y=(1.2)^{\frac{t}{10}}$, and classify them as representing exponential growth or decay.
F-BF.1. Write a function that describes a relationship between two quantities.★
- Determine an explicit expression, a recursive process, or steps for calculation from a context.
- Combine standard function types using arithmetic operations. For example, build a function that models the temperature of a cooling body by adding a constant function to a decaying exponential, and relate these functions to the model.
F-LE.1. Distinguish between situations that can be modeled with linear functions and with exponential functions.
- Prove that linear functions grow by equal differences over equal intervals, and that exponential functions grow by equal factors over equal intervals.
- Recognize situations in which one quantity changes at a constant rate per unit interval relative to another.
- Recognize situations in which a quantity grows or decays by a constant percent rate per unit interval relative to another.
F-LE.2. Construct linear and exponential functions, including arithmetic and geometric sequences, given a graph, a description of a relationship, or two input-output pairs (include reading these from a table).
F-LE.3. Observe using graphs and tables that a quantity increasing exponentially eventually exceeds a quantity increasing linearly, quadratically, or (more generally) as a polynomial function.
F-LE.5. Interpret the parameters in a linear or exponential function in terms of a context.
Misconceptions
Student Misconceptions and Common Errors
- Students struggle with function notation, specifically the f(x) and an notation. Some students think that f(5) means a variable f multiplied by 5 rather than knowing that f(5) is the value of the dependent variable y when the value of the independent variable x is 5. The an notation is typically used in situations when the independent variable n is an integer. a7 can also be thought of as the value of the dependent variable when the independent variable n is 7, but it can also be named the value of the 7th term.
- Students use the vertical line test as the definition of a function rather than a method for determining if a graph of a relation plotted on a coordinate plane is a function or not. This overgeneralization fails to work if the members in a set are not numbers and cannot be plotted on a coordinate plane or when defining functions parametrically. The graph of the parametric function v(t) = 2cos(t) is a circle and does not pass the vertical line test but it is still a function.
- 'Graph as a picture' confusion occurs when students believe that the graph of a relationship between two variables is the actual picture of the situation. For example, suppose a ball is thrown straight up in the air and allowed to drop to the ground. The relationship between the time in the air and height of the ball is a parabola but the actual path of the ball follows a vertical line. Many students think that the path of the ball follows a parabola when actually only the relationship between time and height is parabolic. This problem also shows up when students are asked to sketch the graph of height of a person riding on a Ferris wheel as a function of time. Many students will draw a circle to represent the relationship rather than the periodic function that it is.
- Restricting the domain of functions to avoid division by zero is difficult for many students. Students do not necessarily have trouble finding the restricted values but fail to understand why division by zero is undefined.
Vignette
In the Classroom
- The vignette below describes a classroom activity to help students see how two variables relate to each other in an interactive way and then use this information to discuss key features of the concept of function. The teacher wanted to review the definition of a function and the domain of a function with her students and give them ways to think about these ideas in more ways than just memorizing definitions.
|
The teacher introduces a motion detector that is plugged into the computer that is being displayed on the overhead. The motion detector measures the distance an object is from the sensor. If a person moves back and forth in front of the sensor the computer can record the distance the person is from the sensor in meters and the time in seconds since the measurements began. Shelby comes up and moves back and forth as the computer records the distances and displays the graph of distance versus time on the display. Teacher: [Points to the point on the graph.] What does this point represent? Kati: That is where I started. Since the time is zero seconds and the distance is one meter. Shelby was about 1 meter away from the clicker thing when you started recording. Teacher: [Point to the point (3 seconds, 2 meters) on the graph.] What does this point represent? Richard: That is where Shelby was at 3 seconds. Teacher: Where was she, Richard? Richard: She was two meters from the clicker. Teacher: Is the clicker in the sensor correct? Richard: Yes. Teacher: Think about how the graph shows how Shelby moved back and forth. Sketch the graph in your notes and write down how the graph shows Shelby's movement. |
Resources
Teacher Notes
- Instruction involving notation should focus on having both teachers and students use academic language that is clear and specific (e.g. naming f(7) as "the value of the dependent variable y when the value of the independent variable x is 7" or "a11 is the 11th term in a sequence").
- The vocabulary of independent variable and dependent variable needs to be emphasized. Symbolically the convention for identifying the independent and dependent variable is the choice of letters (i.e., using the function y = 3x - 7, x is usually defined as the independent variable and the value of y is typically dependent on the choice of the value of x). Real world situations like the amount of money someone who is paid by the hour makes in a day depends on the number of hours he or she works during that day. In this case the amount of money being paid (dependent variable) depends on the time worked (independent variable). On the other hand if that worker wants to earn a certain amount during the day then the number of hours she works depends on that amount. In many situations either variable can be the independent variable, which causes confusion among teachers and students. Instruction should emphasize that the selection of which variable is independent is mostly based on which one is the easiest to calculate (e.g., in 2w = v, w would be selected as the independent variable since finding the value of v when w is 7 is easier to calculate than finding the value of w when v is 11), unless it is clear from the situation that one variable is the one being manipulated.
- Evaluating functions (e.g., find f(4) if f(x) = x2 + 3x) is more arithmetic than algebraic since only the order of operations need to be followed). On the other hand, students should also be asked to find the value(s) of the independent variables given the function rule and the value of the dependent variable (e.g., find x when f(x) = 10 if f(x) = x2 + 3x. This problem is more algebraic since it asks students to solve an equation. The benchmark for this standard only states that students are able to evaluate a function by using a value for the independent variable from the domain and finding the matching value of the dependent variable, but students should be asked to move fluently in both directions.
- Students often ask why the "exactly one" part of the definition of a function is important and it is often the only characteristic that is used to determine whether a relation is a function or not. This characteristic developed over many years for a variety of reasons, but practically it is important because if $f(5)$ is written it should be clear what is being communicated and therefore should only represent one value. If $f(x)=\pm\sqrt{x+11}$ (this is a relation that is not a function) then $f(5)$ could represent either 4 or -4. The avoidance of this confusion is one of the main reasons for the exactly one characteristic of a function.
- 'Graph as a picture' confusion is common among students. A motion detector connected to a computer or a graphing calculator can be used to help students see graphically the relationship between two variables as they move themselves or an object around. Making connections between the movements of the object and the features of the graph show that the graph highlights the movement of the object but does not necessarily match the actual path of the object.
- Rational functions like $f(x)=\frac{1}{x-5}$ have a restricted domain to avoid division by zero. Teachers can help students make sense of why division by zero is undefined by using examples emphasizing the relationship between multiplication and division. Many students will say that $\frac{20}{4}$ is 5 because 5 × 4 = 20. It follows that $\frac{0}{7}$ is 0 because 0 × 7 = 0. Many students will explain that $\frac{5}{0}$ is equal to 0. This leads to a contradiction, because if $\frac{5}{0}$ = 0 then 0 × 0 = 5, which is not true. As students search for values for $\frac{5}{0}$ they should see that they are trying to solve the equation a × 0 = 5, which has no solution; therefore, division by zero must be undefined. The graphs of functions provide additional evidence that division by 0 is undefined.
Function Matching
Finding the Function Expression That Matches a Generated Function Graph
Domain Representations
Students use graphs, tables, number lines, verbal descriptions, and symbols to represent the domain of various functions.
Movement with Functions
This three-lesson unit focuses on helping students describe how features of movement like speed and position are represented in tables, graphs and equations.
Additional Instructional Resources
Movement with Functions
This three-lesson unit focuses on helping students describe how features of movement like speed and position are represented in tables, graphs and equations.
- function
- domain
- range
- independent variable
- dependent variable
- undefined
Professional Learning Communities
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
- How do my students explain the difference between an independent variable and a dependent variable?
- What types of experiments or manipulatives can I use to help my students explore functional relationships?
- Do my students understand why the "exactly one" part of the definition of a function is important?
- Are my students able to distinguish between functions and non-functions using tables, graphs, and equations?
Materials
Developing Essential Understanding of Functions Gr. 9-12 (NCTM, 2010)
Focus in HS Mathematics: Reasoning and Sense Making in Algebra (NCTM, 2010
Common Core State Standards (http://www.corestandards.org/the-standards/mathematics)
Ruddell, M.R., & Shearer, B.A. (2002). Middle school at-risk students become avid word learners with the vocabulary self-collection strategy (VSS). Journal of Adolescent & Adult Literacy, 45, 352-363.
Assessment
|
Example Item 1
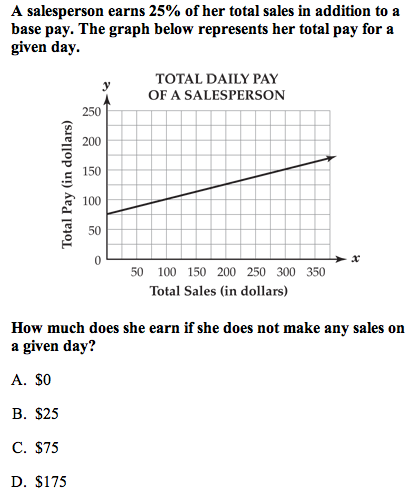
Source: Maryland High School Assessment Algebra/Data Analysis - Item 49 Correct Answer: C Cognitive Level: Knowledge |
||||
|
Example Item 2
Source: Maryland High School Assessment Algebra/Data Analysis - Item 27 Correct Answer: C Cognitive Level: Knowledge |
||||
|
Example Item 3 Which graph shows a function?
Source: MCAII Item Sampler 11th Grade Mathematics Correct Answer: B Cognitive Level: Knowledge |
||||
|
Example Item 4
Correct Answer: B Cognitive Level: Knowledge
Correct Answer: C Cognitive Level: Knowledge
Correct Answer: B Cognitive Level: Knowledge
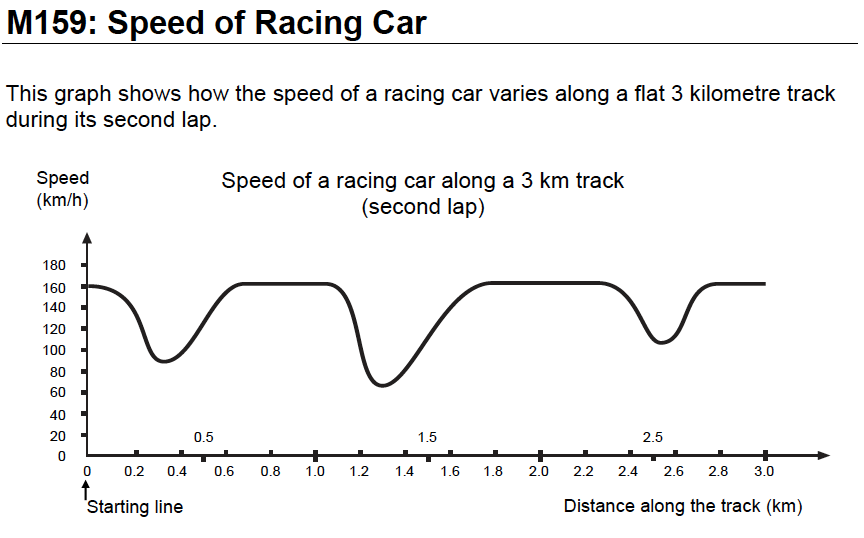
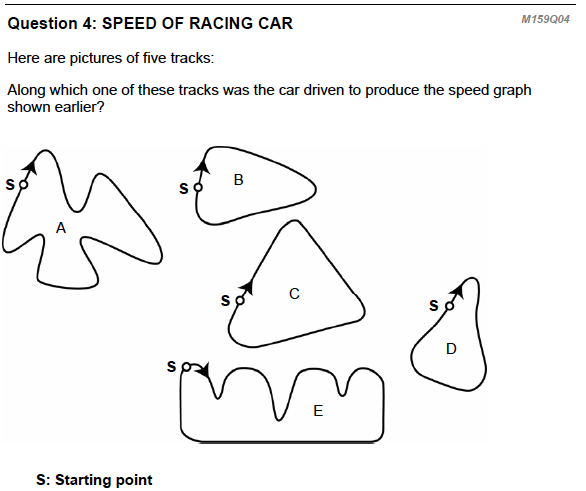
Correct Answer: B Cognitive Level: Application, Analysis, Synthesis and Evaluation Source: Programme for International Student Assessment (PISA) released item - M159 |
Differentiation
- Students with language and/or information processing difficulties and EL students benefit from the use of vocabulary development, guided notes, concept maps, and other graphic organizers when integrated with mathematics instruction. Teachers can find an excellent resource in the use of these tools in mathematics in the following:
Barton, M. L., & Heidema, C. (2002). Teaching reading in mathematics: A supplement to teaching reading in the content areas teacher's manual. (2nd ed.). Aurora, CO: Mid-continent Research for Education and Learning.
Zike, D. (2003). Dinah Zike's big book of math for middle school and high school. San Antonio, TX: Dinah-Might Adventures, LP. (www.dinah.com)
- Function, range, independent/dependent are all problematic because they are used with other meanings and in other contexts in English (function and range can be both nouns and verbs; range has two meanings in math, the value of the dependent variable and the distance between two numbers). Teachers need to be careful to use these terms very carefully and to be explicit about the context. Use as many non-linguistic approaches as possible - demonstrations, manipulatives, pictures, etc. Have students create their own math dictionaries including definitions they create, pictures, and examples of the terms. Promote the use of the Frayer model, verbal/visual maps, graphic organizers, and foldables to make sense of new vocabulary. Having a word wall in the math classroom to refer to can be helpful.
Resources for teachers of English Language Learners in Math:
Echevarria, J. J., Vogt, M. E., & Short, D. J. (2009). The SIOP model for teaching mathematics to English learners. Columbus, OH: Allyn & Bacon.
Kersaint, G., Thompson, D. R., & Petkova, M. (2009). Teaching mathematics to English language learners. New York: Routledge.
Texas State University System. (2004). Mathematics for English language learners. Retrieved from http://www.tsusmell.org/ .
This website includes online teaching videos showing best practices along with a classroom lesson bank.
- The standards emphasize functions as a special relation between two sets. In most high school settings the sets are the sets of real numbers and the rules are mathematical formulas. Students should understand that functions can also connect sets of objects or shapes and the relation is a transformation. Matrices can also be objects in a function.
Parents/Admin
Administrative/Peer Classroom Observation
|
Students are: |
Teachers are: |
|
using real-world contexts or manipulatives to observe how changes in one variable influence the changing of another variable. |
actively engaging their students to explore relationships between variables that are not functions and relationships that are functions. |
|
using language to describe the meaning of functions notation such as |
using vocabulary that helps students make sense of notation such as saying "the value of the dependent variable when the independent variable is 3" when referring to the notation |
|
able to distinguish relations that are functions from ones that are not when represented using a table, graph, equation, or a real-world setting. |
not using the vertical line test as the definition of a function. |
Parent Resources
Double or Not?
This is an activity that students can do with their parents to explore the relationship between time and amount paid under a certain payment plan.
Interactivate
This web site provides java applets that allow students to investigate mathematical ideas in dynamic ways.
References
Bush, W.S. (Ed.). (2000). Mathematics assessment: Cases and discussion questions for grades 6-12.
Bush, W. S., & Greer, A. S. (Eds.). (1999). Mathematics assessment: A practical handbook for grades 9-12.
National Council of Teachers of Mathematics. (2010). Developing essential understandings of functions - Grades 9-12. Reston, VA: NCTM.
See Why the Graph Breaks in NCTM's Mathematics Assessment: Cases and Discussion Questions for Grades 6-12 (p. 24-27; teacher notes on p. 100-102).
See The Golf Shot in NCTM's Mathematics Assessment: A Practical Handbook for Grades 9-12 (p. 123).