8.2.4B Solve & Represent Equations, Inequalities, & Systems
Solve multi-step equations in one variable. Solve for one variable in a multi-variable equation in terms of the other variables. Justify the steps by identifying the properties of equalities used.
For example: The equation 10x + 17 = 3x can be changed to 7x + 17 = 0, and then to 7x = -17 by adding/subtracting the same quantities to both sides. These changes do not change the solution of the equation.
Another example: Using the formula for the perimeter of a rectangle, solve for the base in terms of the height and perimeter.
Solve linear inequalities using properties of inequalities. Graph the solutions on a number line.
For example: The inequality -3x < 6 is equivalent to x > -2, which can be represented on the number line by shading in the interval to the right of -2.
Represent relationships in various contexts with equations and inequalities involving the absolute value of a linear expression. Solve such equations and inequalities and graph the solutions on a number line.
For example: A cylindrical machine part is manufactured with a radius of 2.1 cm, with a tolerance of 1/100 cm. The radius r satisfies the inequality |r - 2.1| ≤ .01.
Represent relationships in various contexts using systems of linear equations. Solve systems of linear equations in two variables symbolically, graphically and numerically.
For example: Marty's cell phone company charges $15 per month plus $0.04 per minute for each call. Jeannine's company charges $0.25 per minute. Use a system of equations to determine the advantages of each plan based on the number of minutes used.
Understand that a system of linear equations may have no solution, one solution, or an infinite number of solutions. Relate the number of solutions to pairs of lines that are intersecting, parallel or identical. Check whether a pair of numbers satisfies a system of two linear equations in two unknowns by substituting the numbers into both equations.
Use the relationship between square roots and squares of a number to solve problems.
For example: If $\pi x^{2}=5$, then $\left | x \right |=\sqrt{\frac{5}{\pi}}$, or equivalently, $x=\sqrt{\frac{5}{\pi}}$ or $x=-\sqrt{\frac{5}{\pi}}$. If x is understood as the radius of a circle in this example, then the negative solution should be discarded and $x=\sqrt{\frac{5}{\pi}}$.
Overview
Standard 8.2.4 Essential Understandings
At this point in their learning, students are familiar with proportional relationships. They have used tables, graphs and equations to represent and solve problems that involve proportional relationships. In this standard, students use this background to move into representing and solving linear equations and inequalities. It is essential for students to make connections to real situations in order to make sense out of this representation. Students need to be able to use information to find the rate of change and the y-intercept and then write the equation describing the relationship represented in the situation. Once students can write the equations and inequalities, the focus is on solving. Students will explore solving linear equations, inequalities, equations containing absolute value, and equations with the variables being squared. It is important for students to continue looking at tables and graphs as well as symbolic representations to find their solutions. Sense-making comes when they can see the solutions in more than one representation. It is crucial for students to be comfortable using the graph and table to find solutions as they move into solving systems of equations and inequalities. The graph paints a picture of the situation and solution that is more of a visual representation for students. When working with just the symbolic method, the meaning of the solution is often lost. Knowing if their answer makes sense is an essential part of students' understanding when solving equations and inequalities.
All Standard Benchmarks
8.2.4.1
Use linear equations to represent situations involving a constant rate of change, including proportional and non-proportional relationships.
For example: For a cylinder with fixed radius of length 5, the surface area A = 2π(5)h + 2π(5)2 = 10πh + 50π, is a linear function of the height h, but the surface area is not proportional to the height.
8.2.4.2
Solve multi-step equations in one variable. Solve for one variable in a multi-variable equation in terms of the other variables. Justify the steps by identifying the properties of equalities used.
For example: The equation 10x + 17 = 3x can be changed to 7x + 17 = 0, and then to 7x = -17 by adding/subtracting the same quantities to both sides. These changes do not change the solution of the equation.
Another example: Using the formula for the perimeter of a rectangle, solve for the base in terms of the height and perimeter.
8.2.4.3
Express linear equations in slope-intercept, point-slope and standard forms, and convert between these forms. Given sufficient information, find an equation of a line. For example: Determine an equation of the line through the points (-1,6) and ([math[\frac{2}{3}$, [math[\frac{-3}{4}$).
- Items must not have context
8.2.4.4
Use linear inequalities to represent relationships in various contexts.For example: A gas station charges $0.10 less per gallon of gasoline if a customer also gets a car wash. Without the car wash, gas costs $2.79 per gallon. The car wash is $8.95. What are the possible amounts (in gallons) of gasoline that you can buy if you also get a car wash and can spend at most $35?
- Inequalities contain no more than 1 variable
8.2.4.5
Solve linear inequalities using properties of inequalities. Graph the solutions on a number line. For example: The inequality -3x < 6 is equivalent to x > -2, which can be represented on the number line by shading in the interval to the right of -2.
8.2.4.6
Represent relationships in various contexts with equations and inequalities involving the absolute value of a linear expression. Solve such equations and inequalities and graph the solutions on a number line. For example: A cylindrical machine part is manufactured with a radius of 2.1 cm, with a tolerance of 1/100 cm. The radius r satisfies the inequality |r - 2.1| ≤ .01.
8.2.4.7
Represent relationships in various contexts using systems of linear equations. Solve systems of linear equations in two variables symbolically, graphically and numerically. For example: Marty's cell phone company charges $15 per month plus $0.04 per minute for each call. Jeannine's company charges $0.25 per minute. Use a system of equations to determine the advantages of each plan based on the number of minutes used.
8.2.4.8
Understand that a system of linear equations may have no solution, one solution, or an infinite number of solutions. Relate the number of solutions to pairs of lines that are intersecting, parallel or identical. Check whether a pair of numbers satisfies a system of two linear equations in two unknowns by substituting the numbers into both equations.
8.2.4.9
Use the relationship between square roots and squares of a number to solve problems.
For example: If πx2 = 5, then |x| = $\sqrt{\frac{5}{\pi }}$, or equivalently, x = $\sqrt{\frac{5}{\pi }}$ or x = $-\sqrt{\frac{5}{\pi }}$. If x is understood as the radius of a circle in this example, then the negative solution should be discarded and x = $\sqrt{\frac{5}{\pi }}$.
- Allowable notation: ±3
- Items may assess the interpretation of square roots based on the context of the item.
Benchmark Group B - Solve and Represent Equations, Inequalities, and Systems
8.2.4.2
Solve multi-step equations in one variable. Solve for one variable in a multi-variable equation in terms of the other variables. Justify the steps by identifying the properties of equalities used. For example: The equation 10x + 17 = 3x can be changed to 7x + 17 = 0, and then to 7x = -17 by adding/subtracting the same quantities to both sides. These changes do not change the solution of the equation. Another example: Using the formula for the perimeter of a rectangle, solve for the base in terms of the height and perimeter.
8.2.4.5
Solve linear inequalities using properties of inequalities. Graph the solutions on a number line. For example: The inequality -3x < 6 is equivalent to x > -2, which can be represented on the number line by shading in the interval to the right of -2.
8.2.4.6
Represent relationships in various contexts with equations and inequalities involving the absolute value of a linear expression. Solve such equations and inequalities and graph the solutions on a number line. For example: A cylindrical machine part is manufactured with a radius of 2.1 cm, with a tolerance of 1/100 cm. The radius r satisfies the inequality |r - 2.1| ≤ .01.
8.2.4.7
Represent relationships in various contexts using systems of linear equations. Solve systems of linear equations in two variables symbolically, graphically and numerically. For example: Marty's cell phone company charges $15 per month plus $0.04 per minute for each call. Jeannine's company charges $0.25 per minute. Use a system of equations to determine the advantages of each plan based on the number of minutes used.
8.2.4.8
Understand that a system of linear equations may have no solution, one solution, or an infinite number of solutions. Relate the number of solutions to pairs of lines that are intersecting, parallel or identical. Check whether a pair of numbers satisfies a system of two linear equations in two unknowns by substituting the numbers into both equations.
8.2.4.9
Use the relationship between square roots and squares of a number to solve problems. For example: If πx2 = 5, then |x| = $\sqrt{\frac{5}{\pi }}$, or equivalently, x = $\sqrt{\frac{5}{\pi }}$ or x = $-\sqrt{\frac{5}{\pi }}$. If x is understood as the radius of a circle in this example, then the negative solution should be discarded and x = $\sqrt{\frac{5}{\pi }}$.
- Allowable notation: ± 3
- Items may assess the interpretation of square roots based on the context of the item.
What students should know and be able to do [at a mastery level] related to these benchmarks
- Students can solve for a variable.
- Students can solve for any variable in a multi-variable equation.
- Students can manipulate equations involving absolute value, squares, and square roots.
- Students will be able to check their answers by substituting the solution back into the original equation.
- Students can solve linear inequalities.
- Students can graph the solution of linear inequalities on a number line.
- Students can graph linear equations.
- Understand that a system with no solutions has parallel lines, a system with one solution has intersecting lines, and a system with infinite solutions is the same line.
Work from previous grades that supports this new learning includes:
- Understand that a closed circle includes the number it represents and therefore is associated with ≤ and ≥.
- Understand that an open circle does not include the number it represents and therefore is associated with < and >.
- Graph equations
NCTM Standards:
Algebra: Understand patterns, relations, and functions
- Relate and compare different forms of representation for a relationship;
- Represent and analyze mathematical situations and structures using algebraic symbols
- develop an initial conceptual understanding of different uses of variables;
- explore relationships between symbolic expressions and graphs of lines, paying particular attention to the meaning of intercept and slope;
- use symbolic algebra to represent situations and to solve problems, especially those that involve linear relationships;
- recognize and generate equivalent forms for simple algebraic expressions and solve linear equations
Common Core State Standards (CCSS)
8.F.4 Construct a function to model a linear relationship between two quantities. Determine the rate of change and initial value of the function from a description of a relationship or from two (x, y) values, including reading these from a table or from a graph. Interpret the rate of change and initial value of a linear function in terms of the situation it models, and in terms of its graph or a table of values.
8.EE.7 Solve linear equations in one variable.
8.EE.7b Solve linear equations with rational number coefficients, including equations whose solutions require expanding expressions using the distributive property and collecting like terms.
7.EE.4b Solve word problems leading to inequalities of the form px + q > r or px + q < r, where p, q, and r are specific rational numbers. Graph the solution set of the inequality and interpret it in the context of the problem. For example: As a salesperson, you are paid $50 per week plus $3 per sale. This week you want your pay to be at least $100. Write an inequality for the number of sales you need to make, and describe the solutions.
8.EE.8 Analyze and solve pairs of simultaneous linear equations.
8.EE.8a Understand that solutions to a system of two linear equations in two variables correspond to points of intersection of their graphs, because points of intersection satisfy both equations simultaneously.
8.EE.8b Solve systems of two linear equations in two variables algebraically, and estimate solutions by graphing the equations. Solve simple cases by inspection. For example, 3x + 2y = 5 and 3x + 2y = 6 have no solution because 3x + 2y cannot simultaneously be 5 and 6.
8.EE.8c Solve real-world and mathematical problems leading to two linear equations in two variables. For example, given coordinates for two pairs of points, determine whether the line through the first pair of points intersects the line through the second pair.
8.EE.2 Use square root and cube root symbols to represent solutions to equations of the form x2= p and x3 = p, where p is a positive rational number. Evaluate square roots of small perfect squares and cube roots of small perfect cubes. Know that $\sqrt{2}$ is irrational.
Misconceptions
Student Misconceptions and Common Errors
- When writing solutions to inequalities, students will show that the answer is greater than 4, but then they will record their answer as 5 or greater. Students think the answer is the next whole number, ignoring all the numbers between 4 and 5 that are also part of the solution.
- Students may think that the inequality symbols indicate the direction of the shading of the number line.
- Students may forget to switch the direction of the inequality symbol (aka "flip" the inequality symbol) when multiplying or dividing by a negative number when solving.
- Students will forget to find both solutions when solving with absolute values.
- Students forget that the solution for a system of linear equations is the point of intersection of the two lines on a graph and only solve for one variable.
- When solving x2 = 81, students recognize that x can equal 9, but sometimes forget that x can also equal -9.
Vignette
In the Classroom
In this problem, students will be exploring possible pledge plans for walking in a walk-a-thon to raise money for their student council. They will be comparing two different plans. In Plan A, walkers will get paid a $4 donation no matter how far they walk and then an additional $2 for each mile they walk. In Plan B, walkers will receive a $10 donation and then an additional $0.50 for each mile they walk.
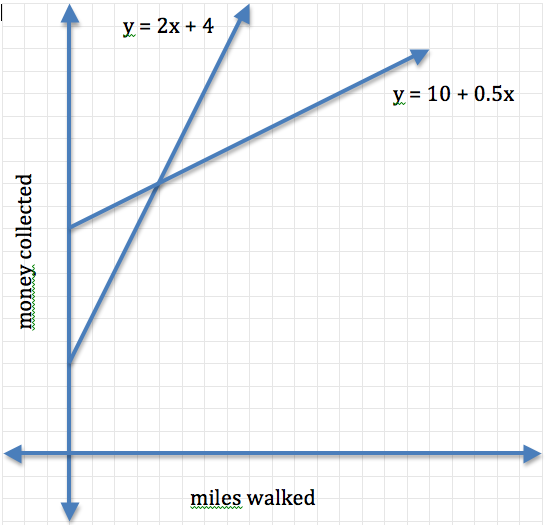
Teacher: Let's look at these two pledge plans. Yesterday we talked about deciding when one is better than the other. So according to these equations, which pledge plan is better?
Student: Well it depends. It depends on how far you walk.
Teacher: So when is Plan A better?
Student: Anytime after 4 miles because the amount of money collected is higher. But before that Plan B is better because the money collected for that Plan is higher.
Teacher: How did you come up with 4 miles?
Student: Well, that's where the lines cross each other or intersect. That point is where the two plans are equal. They will collect the same amount of money if they walk 4 miles.
Teacher: How much money will they collect?
Student: They will collect $12 because that's the y value of the coordinate pair.
Teacher: Ok, so we can look at the graph and find the intersection point to help us find when the two plans are equal. We have also solved this symbolically by making the two plans equal to each other. Try that and see if your answers match.
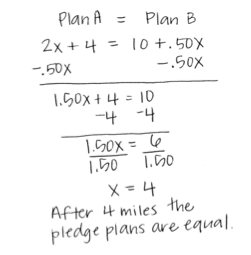
Student: Yes it does!
Teacher: Ok so now let's go back to the question earlier about which plan is better. When is plan A better than Plan B?
Student: Like we said before, anytime after 4 miles. The graph for line A is higher than the graph for line B after that point.
Teacher: We need a way to write "anytime after 4 miles" mathematically to include all the possible solutions.
Student: The miles walked are greater than 4 so I could use the "greater than" symbol: x > 4 miles.
Student 2: I wrote that the miles walked would have to be 5 or more miles because it can't be 4. So I wrote it like this: x ≥ 5 miles.
Teacher: Are these two solutions the same?
Student: I'm not really sure.
Teacher: Let's look at your solutions on a number line. Are they the same?
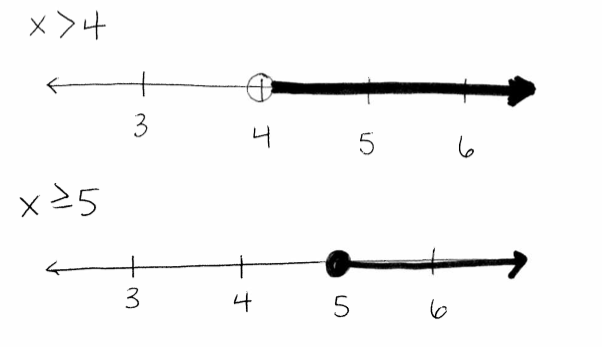
Student: Well, kinda...it has to be greater than 4 miles and the next mile is 5. So it works to be 5 miles or greater.
Teacher: What if the students walked 4.5 miles or 4.2 miles? Will Plan A still be better?
Student: Well, yeah because it's more than 4 miles.
Teacher: Do both of your solutions include 4.5 miles as a possible solution?
Student: Ok, so x > 4 miles does but x ≥ 5 miles doesn't.
So I guess they are not the same. There are a lot of numbers between 4 and 5 that I didn't include in the solution. But I guess we could walk part of a mile. I guess I can't just jump to the next whole number. I have to say that it's just greater than 4 miles. And that's right because it doesn't include 4 miles but still considers all the numbers between 4 and 5.
Teacher: Now that we worked that out, let's go back to checking this solution symbolically. When we were finding the point where the two plans were equal, we used the graph and then checked it by making the equations equal to each other and solving it symbolically. We can do the same thing to check our answer to the question "When is Plan A better than Plan B?" Instead of writing an equation, we write an inequality to represent this situation.
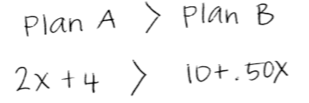
Student: So then what, do we just solve it like the equation?
Teacher: Let's try it. See if we get an answer that matches the answer we got using the graph.
Annie: I got the same answer as the graph. So I just do the same thing I do to solve an equation.
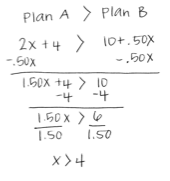
Stan: Wait. I did the same thing that I do to solve equations and my answer doesn't match the graph. I got that x < 4. What did I do wrong? I still got 4 miles but the sign is wrong.
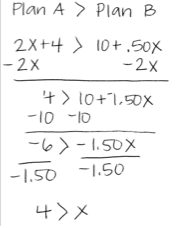
Teacher: What do you notice about the work of these two students?
Student: Well they both did their work correctly. They just started with a different step. Annie subtracted .50x from both sides and Stan subtracted 2x from both sides. So then one ended up with a positive number of "x's" and one with a negative number of "x's."
Student: Yeah, and then Annie has the "x's" on the left and Stan has the "x's" on the right. So which is correct? Annie's matches the graph and Stan's would be right if we just changed the sign around. If you don't have the graph, how do you know which one is right?
Teacher: Let's go back and look at some numbers and compare some numbers and explore what happens when we operate with those numbers. Start with this comparison...
5 > 2 Do you agree with this statement? (Students "yes")
Now multiply both numbers by 3.
15 > 6 Do you agree with this statement? (Students "yes")
Now subtract both numbers by 12
3 > -6 Do you still agree? (Students "yes, what's the point?")
Ok, now multiply both by -4.
-12 > 24 Do you still agree?
Students: No, that's not right because -12 is less than 24. It should be written like -12 < 24. What happened?
Teacher: Let's keep going with this new true statement.
-12 < 24
Add -4 to both numbers.
-16 < 20
Is this still true? (Students "yes"). Divide both numbers by -2.
8 < -10. Is this still true?
Students: No, that's not right again. 8 is greater than -10 so it should be written
8 > -10. What's the deal?
Teacher: Anyone notice anything? What keeps making the statement false?
Student: It seems like something with negative numbers. Like when we multiplied by
-4, but then we added negative 4 and it wasn't a problem.
Teacher: Let's look at the whole train of operations and see if we can notice any patterns.

Student: We circled the places where we ran into trouble. The only times were when we multiplied and divided by a negative number. The first operation we did was multiply by 3 and there was no problem. So I think it gets messed up whenever we multiply or divide by a negative number.
Teacher: Let's all check this conjecture. Start with a true inequality statement. Do four operations. Make sure at least one of your operations divides or multiplies by a negative number.

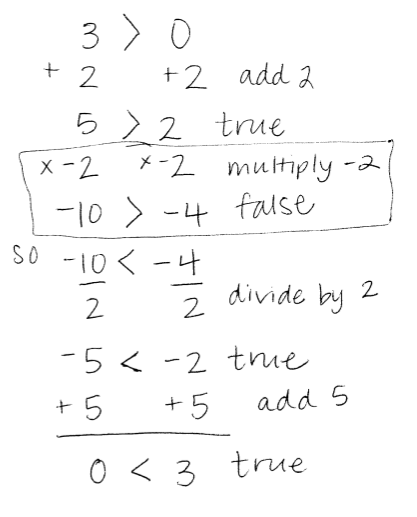

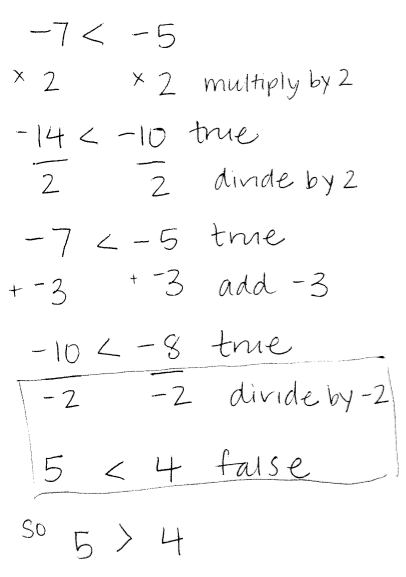
Student: Yeah it works for all of them! When you multiply or divide by a negative number, you have to make it "work" by changing the sign.
Teacher: How does this help us understand what Annie and Stan did symbolically to prove that the pledge Plan A is better than Plan B when they walk more than 4 miles in the walk-a-thon?
Student: If you look at their work, Annie never had to divide by a negative number and Stan did. So he should make it "work" by changing the sign. We even said that earlier. We said Stan would be right if he could change the sign.
Teacher: Let's try it out with another set of equations. This time let's start with finding the solution symbolically and check our solution using the graph. We will have to pay close attention to the operations we use to solve so we make sure we consider the discovery you just made as to what happens when you divide or multiply by a negative number.
Resources
Teacher Notes
Students may need support in further development of these previously studied concepts and skills:
- use the number line when showing the solution to an inequality so they can see all possible answers and don't unintentionally leave out possible solutions.
- connect solutions for the inequalities to the words that describe the solutions, to help students make sense of the inequality symbol.
- give students opportunities to understand why the inequality sign changes direction when multiplying and dividing by a negative number. Avoid just telling them the rule. See vignettes below:
Vignettes
There is a rule that states that when you divide or multiply an inequality by a negative number you must reverse the direction of the inequality. So who died and made this rule a rule? Where's the rhyme or reason to this? To check the validity of the rule, let's go back to where we had 6 > -x. Instead of multiplying through by -1, let's do something else. Let's add x to both sides. Thus we get 6 + x > 0, 0 because x + -x on the right cancel to yield 0. Now subtract 6 from both sides to get x > -6. Voila! Now we see why the rule rules. Multiplying through an inequality by -1 changes the position of the variable from one side to the other, basically causing the inequality symbol to face the other way. This does not happen with equations because both the right and left sides are in balance and are therefore indistinguishable.
- When working with absolute value, tie it back to the number line. Students need to remember that absolute value represents the distance from zero. For example, on the number line there are 2 places that can be 10 away from zero. See link from Cool Math website.
- When solving systems, continue to connect to the graph. This will help remind students that the solution is the point of intersection. This will also help students make sense of a system that has no solution because the lines are parallel, or systems that have infinite solutions because the equations represent the same line.
- When students are graphing inequalities on a number line, be intentional about having them graph inequalities where the variable is written before the inequality symbol and where the variable is written after the inequality symbol; e.g., x ≤ 4 and 10 ≤ x. It is helpful to teach students to either rewrite the inequality so the variable comes before the inequality symbol, or help them remember to always read it as a sentence starting "x is..." For example, "x is greater than or equal to 10 instead of "10 is less than or equal to x."
- Students need to be reminded to always check their work when solving for a variable in an equation. When checking their answer have students put a question mark on top of the equal sign after they plug in the value of their answer for the variable.
- After students learn the rule of changing the inequality symbol when multiplying or dividing by a negative number, they will sometimes mistakenly change the inequality symbol when they should not. Sometimes they change the inequality symbol when they divide INTO a negative value and not divide BY a negative value. Ex: 4x ≤ -16 To solve this inequality students need to divide both sides by 4. The solution would then be x ≤ -4, but students see the negative and think they should switch the inequality symbol.
- There are a variety of methods for solving systems of equations (graphing, using a table, substitution, combination/elimination). Depending on the form the original equations are given in, one method may be more efficiently used to solve than the others. Although any method could be used, expose students to a variety of methods and let them choose which method is most efficient to solve the system.
- Starting from the concrete notion of weights and balances and moving to symbolic expressions and representations of functions, this i-Math investigation has focused on some of the issues that arise along the way. In this part, this connection is extended to functions. More sophisticated tools allow for a greater diversity of investigations.
- Using tiles to represent variables and constants, learn how to represent and solve algebra problems. Solve equations, substitute in variable expressions, and expand and factor. Flip tiles, remove zero pairs, copy and arrange, and make your way toward a better understanding of algebra.
- Talk or Text, Solving Systems. In this lesson, students compare different costs associated with two cell phone plans. They write equations with 2 variables and graph to find the solution of the system of equations. They then analyze the meaning of the graph and discuss other factors involved in choosing a cell phone plan.
- Pan-Balance Numbers. Use this tool to strengthen understanding and computation of numerical expressions and equality. In understanding equality, one of the first things students must realize is that equality is a relationship, not an operation. Many students view "=" as "find the answer." For these students, it is difficult to understand equations such as 11 = 4 + 7 or 3 × 5 = 17 - 2.
- Movement with Functions. In this lesson, students use remote-controlled cars to create a system of equations. The solution of the system corresponds to the cars crashing. Multiple representations are woven together throughout the lesson, using graphs, scatter plots, equations, tables, and technological tools. Students calculate the time and place of the crash mathematically, and then test the results by crashing the cars into each other.
Additional Instructional Resources
- A web blog focused on formative assessment.
- A website with a variety of different math graphic organizers, including solving systems of equations by combination or substitution.
- Students solve systems of 2-by-2 linear equations using tables, graphs and substitution. The lesson builds on previous experiences with problem situations represented and solved using a system of equations. Students practice more formal strategies for representing and solving systems of equations.
- This applet investigates solving simple linear equations by balancing both sides using four operations.
- This virtual manipulative allows you to solve simple linear equations using a balance beam.
system of equations: A collection of two or more equations with a same set of unknowns. In solving a system of equations, try to find values for each of the unknowns that will satisfy every equation in the system.
undefined: Systems have no solution when the lines are parallel (i.e., have the same slope) and the lines have different y-intercepts.
infinite: Systems have infinite solutions when the lines have the same slope and the same y-intercept. If two lines have the same slope (i.e., are parallel) and the same y-intercept, they are actually the same exact line. In other words, systems have infinite solutions when the two lines are the same line.
intersecting: Two lines are intersecting if they only touch at one point. The solution to a system of linear equations that are intersecting is a coordinate pair.
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
- How can I be certain students understand why the inequality is switched when multiplying or dividing by a negative number, and what can I do to help when students aren't understanding?
- What evidence exists that students can successfully solve a system of equations and understand the meaning of the solution in the original context?
- How effectively did the lesson involve students in reasoning and problem solving? Explain. What changes could you make to encourage more student reasoning and problem solving?
- What parts of the lesson were challenging to students? What was the source of students' difficulties? How did you handle these situations? How might you more effectively handle these challenges if you taught the lesson again?
Materials
The following three websites explore effective strategies for teaching important skills and concepts in Algebra 1. They help you examine teaching practices through a combination of video, print, and Web-based activities.
Comparing linear functions: Lesson planning (part A). (n.d.). The Inside Mathematics website. Retrieved June 12, 2011, from http://www.insidemathematics.org/index.php/classroom-video-visits/publi…
Focus in grade 8: Teaching with curriculum focal points. (2010). Reston, VA: National Council of Teachers of Mathematics.
Hendrickson, K. (n.d.). Equations of attack. Illuminations. Retrieved June 13, 2011, from http://illuminations.nctm.org/LessonDetail.aspx?id=L782
Insights into Algebra 1 workshop 1. (n.d.). Retrieved June 12, 2011, from http://learner.org/workshops/algebra/workshop1/index.html?pop=yes&pid=2…
Intoduction-Algebra. (n.d.). California Department of Education. Retrieved June 13, 2011, from http://www.cde.ca.gov/ta/tg/sr/documents/cstrtqalgebra.pdf
Math graphic organizers: A teachers' page. Retrieved June 12, 2011, from http://www.dgelman.com/graphicorganizers/#ALGI
McShea, B., Vogel, J., & Yarnevich, M. (2005, April). Harry Potter and the Magic of Mathematics. Mathematics Teaching in the Middle School, 10, 408.
Principles and standards for school mathematics. (2000). Reston, VA: National Council of Teachers of Mathematics.
Regents Exam Questions A.A.23: Transforming Formulas 2. (n.d.). Jefferson Math Project. Retrieved June 13, 2011, from www.jmap.org/JMAP/RegentsExamsandQuestions/3-AdobePDFs/WorksheetsByPI-T…
Assessment
9 questions on solving linear inequalities with one variable.
Source: http://www.jmap.org/JMAP/RegentsExamsandQuestions/3-AdobePDFs/WorksheetsByPI-Topic/IntegratedAlgebra/Algebra/A.A.24.SolvingInequalities.pdf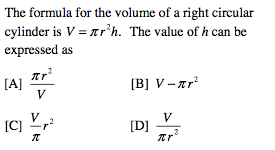
Regents Exam Questions A.A.23: Transforming Formulas 1
http://www.jmap.org/JMAP/RegentsExamsandQuestions/3-AdobePDFs/WorksheetsByPI-Topic/IntegratedAlgebra/Algebra/A.A.23.TransformingFormulas1.pdf
Correct answer: D
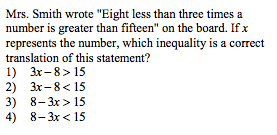
Integrated Algebra Regents Exam 0808
http://www.jmap.org/JMAP/RegentsExamsandQuestions/3-AdobePDFs/CompactExams/IntegratedAlgebra/0808ExamIA_EV.pdf
Correct answer: 1

California Algebra I Standards Test released questions
http://www.cde.ca.gov/ta/tg/sr/documents/cstrtqalgebra.pdf
Correct answer: D
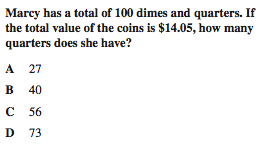
Taken from California Algebra I Standards Test released questions
http://www.cde.ca.gov/ta/tg/sr/documents/cstrtqalgebra.pdf
Correct answer: A

California Algebra I Standards Test released questions
http://www.cde.ca.gov/ta/tg/sr/documents/cstrtqalgebra.pdf
Correct answer: A

California Algebra I Standards Test released questions
http://www.cde.ca.gov/ta/tg/sr/documents/cstrtqalgebra.pdf
Correct answer: B
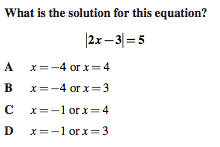
California Algebra I Standards Test released questions
http://www.cde.ca.gov/ta/tg/sr/documents/cstrtqalgebra.pdf
Correct answer: C

California Algebra I Standards Test released questions
http://www.cde.ca.gov/ta/tg/sr/documents/cstrtqalgebra.pdf
Correct answer: D
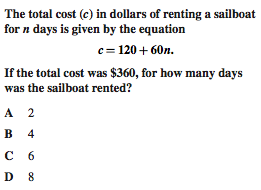
California Algebra I Standards Test released questions
http://www.cde.ca.gov/ta/tg/sr/documents/cstrtqalgebra.pdf
Correct answer: B
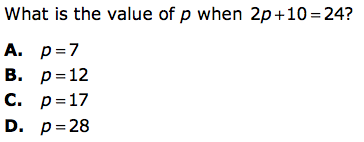
Correct answer: A
Minnesota MCA III 8th grade Sample Problems
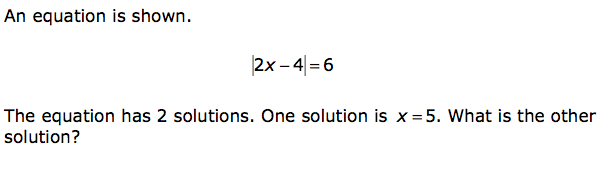
Correct answer: -1
Minnesota MCA III 8th grade Sample Problems
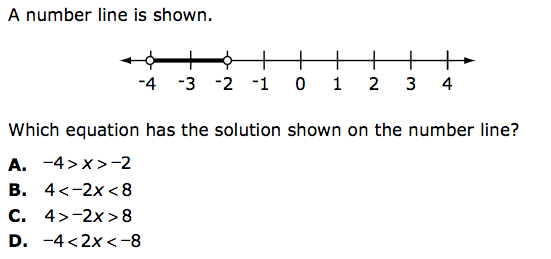
Correct Answer B
Minnesota MCA III 8th grade Sample Problems
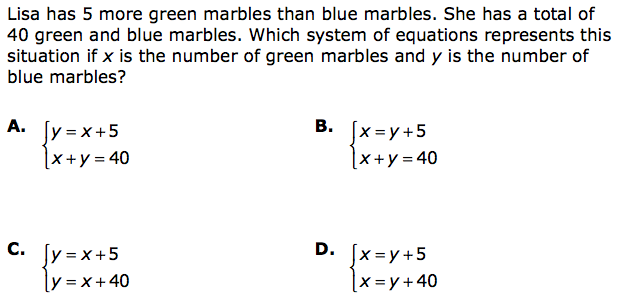 Correct Answer B
Correct Answer B
Minnesota MCA III 8th grade Sample Problems
Differentiation
- When teaching solving an equation for a variable, introduce the concept with manipulatives such as blocks and chips or an online manipulative so students understand the concept of maintaining equality. After students understand solving with manipulatives, have them make the connection to solving equations without manipulatives.
- Use graphic organizers to help with processes using steps that need to be followed. http://www.sw-georgia.resa.k12.ga.us/Math.html has a variety of graphic organizers for these benchmarks, including how to solve a system of equations by substitution, how to solve a system of equations by linear combination, and finding slope.
- Use graphic organizers to help with processes that have steps that need to be followed. http://www.sw-georgia.resa.k12.ga.us/Math.html has a variety of graphic organizers for these benchmarks, including how to solve a system of equations by substitution, how to solve a system of equations by linear combination, and finding slope.
Systems with more than 2 equations.
Have students write and solve systems of inequalities
Parents/Admin
Administrative/Peer Classroom Observation
Students Are: | Teachers Are: |
solving systems of equations symbolically and graphing the systems to make sense out of their answers. | using the number line when showing the solution to an inequality so students can see all possible answers and don't unintentionally leave out possible solutions. |
using words to describe the solution to their inequality before writing it mathematically. | connecting solutions to the inequalities to the words that describe the solution, which helps students make sense of the inequality symbol. |
checking their solutions by substituting back into the original equation(s). | avoiding telling students the rule; givng students opportunities to understand why the inequality sign changes direction when multiplying and dividing by a negative number. |
| continuing to connect solutions to the graph, and graphing equations and solutions on the number line. |
| encouraging students to check their answer and make sure it "works" and makes sense in the situation. when solving an equation involving absolute values, always connecting it to the number line, and reinforcing the idea that absolute value is referring to the distance away from zero. |
