7.3.1A Circumference & Area of Circles & Sectors
Demonstrate an understanding of the proportional relationship between the diameter and circumference of a circle and that the unit rate (constant of proportionality) is π. Calculate the circumference and area of circles and sectors of circles to solve problems in various contexts.
Overview
7.3.1 Essential Understandings
As the overarching theme of 7th grade mathematics is proportionality, the placement of circle measurement in 7th grade is intentional. Circles provide the perfect vehicle for deepening students' understanding of proportionality. There are at least 2 specific ways proportionality is evident in circle measurement:
The circumference (C) of a circle is proportional to the radius (r) of the circle. That is, there is some constant k such that for all circles, C = kr. This implies, for instance, that if you double the radius of a circle, then you double its circumference.
The area of a circle is proportional to the square of the radius of the circle. That is, there is some constant h such that for all circles, A = hr2. This implies, for instance, that if you double the radius of a circle, then you quadruple its area.
By decomposing two- and three-dimensional shapes into smaller, component shapes, students find surface areas and develop and justify formulas for the surface areas and volumes of prisms and cylinders. As students decompose cylinders by slicing them, they develop and understand formulas for their volumes (Volume = Area of base × Height). They apply these formulas in problem solving to determine volumes of cylinders. Students see that the formula for the area of a circle is plausible by decomposing a circle into a number of wedges and rearranging them into a shape that approximates a parallelogram. They select appropriate two- and three-dimensional shapes to model real-world situations and solve a variety of problems (including multi-step problems) involving surface areas, areas and circumferences of circles, and volumes of cylinders. (7th Grade NCTM Curriculum Focal Points)
All Standard Benchmarks
7.3.1.1
Demonstrate an understanding of the proportional relationship between the diameter and circumference of a circle and that the unit rate (constant of proportionality) is π. Calculate the circumference and area of circles and sectors of circles to solve problems in various contexts.
7.3.1.2
Calculate the volume and surface area of cylinders and justify the formulas used. For example: Justify the formula for the surface area of a cylinder by decomposing the surface into two circles and a rectangle.
Benchmark Group A - Circumference & Area of Circles ahnd Sectors
Benchmark 7.3.1.1 Demonstrate an understanding of the proportional relationship between the diameter and circumference of a circle and that the unit rate (constant of proportionality) is π. Calculate the circumference and area of circles and sectors of circles to solve problems in various contexts.
What students know and be able to do [at a mastery level] related to these benchmarks
- Find the diameter given the radius or determine the radius given the diameter.
- Find the radius (or diameter) given the circumference of a circle.
- Use the formula to find circumference and area of a circle, or a sector of a circle.
- Describe pi as the ratio of a circle's circumference to its diameter.
- Calculate measurements of a sector.
- Identify the part (fraction or percent) of a circle represented by a given sector.
- Generalize, algebraically, how to find the volume of a cylinder (Volume = area of the base times height or V =πr2h).
Work from previous grades that supports this new learning includes:
- squaring numbers
- using a formula and substituting in values for the unknown variable
- identifying and naming basic two- and three-dimensional shapes, such as squares, circles, triangles, rectangles, trapezoids, hexagons, cubes, rectangular prisms, cones, cylinders and spheres
- recognizing and drawing a net for a three-dimensional figure
- calculating the surface area and volume of prisms and use appropriate units, such as cm2 and cm3.
- calculating the area of quadrilaterals and triangles
- estimating the perimeter and area of irregular figures on a grid when they cannot be decomposed into common figures .
- determining the rate for ratios of quantities with different units.
- representing the relationship between two varying quantities with function rules, graphs and tables
- measuring angles/drawing angles of specific degrees using protractors or angle rulers
NCTM Standards
Use visualization, spatial reasoning, and geometric modeling to solve problems:
- use two-dimensional representations of three-dimensional objects to visualize and solve problems such as those involving surface area and volume.
Measurement Standard for Grades 6-8
Understand measurable attributes of objects and the units, systems, and processes of measurement.
- Understand, select, and use units of appropriate size and type to measure angles, perimeter, area, surface area, and volume.
Apply appropriate techniques, tools, and formulas to determine measurements.
- Select and apply techniques and tools to accurately find length, area, volume, and angle measures to appropriate levels of precision;
- Develop and use formulas to determine and circumference of circles and the area of triangles, parallelograms, trapezoids, and circles and develop strategies to find the area of more-complex shapes;
- Develop strategies to determine the surface area and volume of selected prisms, pyramids, and cylinders.
Common Core State Standards (CCSS)
Geometry 7.G Draw, construct, and describe geometrical figures and describe the relationships between them.
7.G.4 Know the formulas for the area and circumference of a circle and use them to solve problems; give an informal derivation of the relationship between the circumference and area of a circle.
7.G.6 Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.
Geometry 8.G Understand congruence and similarity using physical models, transparencies, or geometry software.
8.G.9 Know the formulas for the volume of cones, cylinders and spheres and use them to solve real-world and mathematical problems.
Misconceptions
Student Misconceptions and Common Errors
- Students sometimes believe r2 is the same as r × 2;
- Students will sometimes interchange the formulas for circumference and area;
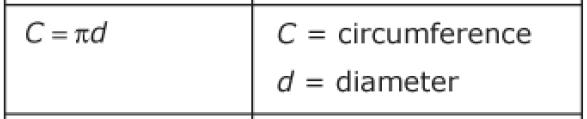

Formulas taken from the Minnesota MCA III 7th Grade Math Formula Sheet.
Note: There are no diagrams given with formulas on the formula sheet. Standard 7.3.1 says students will be able to "justify formulas." Be sure students not only know how to substitute values into the formulas but can also describe how where these formulas came from.
- Students mistakenly use the diameter in the area formula in place radius (r × 2 instead of r2) or square the diameter instead of the radius.
- Students sometimes believe that pi is equivalent to 3.14 versus this being an approximation.
- Students do not label their answers with appropriate units (for example: not using units squared when referring to the area of a circle and/or using units squared for circumference)
Vignette
In the Classroom
Ms. R.: Okay, class, today we are going to do some measuring of objects. You will work with a partner on this activity.
I have placed several circular, spherical, and cylindrical objects on my counter for you to use. You may select any 6 objects. Please do not take all 6 at the same time, as I do not have enough for all groups to each take 6 objects. We are going to measure the distance around the outside edge of each object. What is that value called?
Student A: Perimeter
Ms. R.: Well, that is correct, but don't we call the distance around a round object something else?
Student A: Circumference?
Ms. R.: Yes, that is right. We are going to measure the circumference of each object. How could we measure that distance? We have to be able to go around curves?
Student A: Use string and then place it on a ruler to see how long it is.
Student B: Trace the object and use a ruler.
Student C: Use a tape measure.
Student D: Use a measuring tape that is used for sewing.
Ms. R.: All of those methods would work. What I am going to give you are tape measures that are bendable and can be manipulated easily around these objects. You are going to measure very carefully and measure to tenths. Where are the tenths on the tape measure?
Student E: On the centimeter side.
Student D: They are the little lines between the centimeters.
Ms. R.: How many are between each centimeter?
Student C: 10.
Ms. R.: Right. Now, when you write them, you cannot write $7\frac{1}{4}$, or something like that. Why?
Student B: Because there aren't $\frac{1}{4}$ Centimeters.
Ms. R.: Good. You will be very careful when you measure. You will also measure the diameter of each object. You need to be careful where you place the tape measure. If you place it directly through the center, you actually are not measuring the diameter, because the tape measure will be going through the middle, and where you read it will actually not be the diameter. You need to place the tape measure so the left or right of it runs ALONGSIDE the diameter. You will measure the diameter to the nearest 10th as well. Now if you KNOW what we are trying to do, you cannot just 'cheat' and not do the measurements. I do not want you to use any tricks or shortcuts you may think you know.
Student A: But can't we just measure the diameter and multiply by pi?
Ms. R.: Well, what IS pi?
Student A: 3.14.
Ms. R.: But what IS it?
Student A: A number we multiply by diameter?
Ms. R.: Since we are not sure what that pi is, we will continue to do the lesson this way. Ok, you can start measuring your objects. When you have measured the diameter and circumference, both to the nearest tenth, then you will divide the circumference by the diameter and write its quotient in the table on your paper. Then round this value to hundredths.
Student B: What's a quotient?
Ms. R.: What did I just ask you to do?
Student B: Divide the circumference by the diameter.
Ms. R.: So what do you think a quotient is?
Student B: The answer we'll get when we divide?
Ms. R.: That's exactly right. Remember to round your quotient to hundredths. Go ahead and get started.
As the students engage in this task, Ms. R is walking around the room observing and making sure they are accurately measuring their objects. The students are dividing each circumference/diameter pair as they go, so the teacher can check for errors right away. The quotients should be close to 3.14.
Ms. R.: Oh. Your group got 3.95 for a quotient. Would you please re-measure that object? I think there may be a measurement error."
Identifying a group that has found the quotient 3.14 twice, the teacher asks them how that is possible, and also notices in the partners' tables, that the two students have two different answers for their circumferences.
Ms. R.: How is it possible that you have 2 different answers for your circumference, but you both were able to get 3.14 for your quotient?
Student B: Well, I know we just have to measure the circumference and divide by 3.14 and we get the diameter.
Ms. R.: Why?
Student B: I don't know. You just do.
Ms. R.: I am concerned with your work. We are conducting an experiment to see what happens between actual measured diameters and circumferences. To use data that isn't part of this experiment will make your results false. We must be honest and report our actual findings from our data. You need to find out what your data tells you about the relationship between circumference and diameter.
Let's go back and measure the circumference and diameters of each object, and continue this activity with your actual measured data. Once we have those values, we can divide the circumference by the diameter. Remember, we are doing this so we could perhaps remember WHY the relationship is what it is, and not just memorize something or plug a value into a formula.
Ms. R.: Once you've done all 6 objects, and found all 6 quotients, go ahead and average your quotients. Write that number on your paper. What do you notice?
As Ms. R. circulates around the room, she checks to see that the students are finding the averages correctly. If not, she reviews how to find averages.
Ms. R.: Ok, what do we have for answers?
Calls on several groups to give their averages. (3.10, 3.21, 3.30, 3.15)
Ms. R.: Do you see any particular repeated value?
Student C: Yeah, they're all almost 3.
Ms. R.: Yes, but what else? Anything look familiar? Think about what types of objects we are using. Anything?
Student A: They are all close to 3.14?
Student B: They are really close to pi.
Ms. R: IF we all would have measured exactly on every object, the quotients should have been 3.14. Now, did we? No. But were we relatively close? Right! So, what do you think we can say about the relationship between circumference and diameter of a circle?
Student C: Circumference is always bigger than diameter?
Ms. R.: Yes, but more specifically? What can we say about the values in relationship to one another?
Student D: If we divide the circumference by diameter we will get 3.14?
Ms. R.: So the relationship is the circumference divided by the diameter is 3.14? But isn't that a decimal approximation? Isn't it really pi?
Students: Yes!
Ms. R: Right. But are you ever given the circumference and diameter and have to find that relationship? NO, you are not. You are usually given circumference or diameter, and have to find the other. So, how can we do that? Work with what we know.
Student A: If you know diameter, you can multiply by pi to get circumference or if you know circumference, you can divide it by pi to get the diameter.
Ms. R.: Nice job! Correct! The ratio you will always get for circumference and diameter is pi (3.14). No matter what the size of the circular object, if you divide the circumference by the diameter, you will get pi.
Students now see that to find the circumference of a circle, the diameter must be multiplied by pi.
Resources
Students may need support in further development of previously studied concepts and skills.
- 7th Grade is the first time students are calculating the area and circumference of a circle in the standards.
- It is important to talk about calculator differences between using 3.14 or π or $\frac{22}{7}$ with students. Often students will think they have the wrong answer to a problem if they do a problem using 3.14 for pi and someone else used the pi button on the calculator.
- Teachers need to be aware that the benchmark may involve a problem in which the students are given a part of the circumference, and they have to work backwards to figure out of what part (percent or fraction) of the circle they are finding the area.
- Because of the connection between circle measurement and proportionality it is important for teachers to help students make this connection for themselves. Students should be given the opportunity to collect data on the measurements of multiple circles. After putting this data together into an organized list, students should look for patterns that emerge. It is important for teachers to connect the data in a table to its related graph and equation/rules.
- Teacher should be deliberate in making sure students are performing r2(squared) correctly and not calculating r × 2.
Instructional Resources
- Circle Tool. How do the area and circumference of a circle compare to its radius and diameter? This applet allows you to investigate these relationships in the Introduction and Investigation sections and then hone your skills in the Problems section. Be sure to collect data in a table and graph the results to see the proportional relationship that exists between a circle's circumference and its diameter.
- Computing Pi: The Greek mathematician Archimedes approximated pi by inscribing and circumscribing polygons about a circle and calculating their perimeters. Similarly, the value of pi can be approximated by calculating the areas of inscribed and circumscribed polygons. This activity allows for the investigation and comparison of both methods.
Additional Instructional Resources
- This video explains where the area formula for circles comes from.
- Sir Cumference and the Dragon of Pi, (February 2004), Charlesbridge Publishing. Cindy Neuschwander; Wayne Geehan
- Tutorials and Powerpoint on circumference of a circle with example problems. Membership to TES is free, but must register to use the website.
- Play 3 in a row with area and circumference. Some squares included to work backwards to find radius or diameter. Can be played in pairs, groups, or in two teams with a whole class.
radius: distance from the center of a circle to a point on the circle.
diameter: the length of a straight line passing through the center of a circle and connecting two points on the circle. OR The diameter of a circle is the longest distance across a circle. (The diameter cuts through the center of the circle. This is what makes it the longest distance.)
pi: the ratio of the circumference to the diameter of a circle; approximately equal to 3.1415...
circumference: the circumference of a circle is the perimeter or the distance around the outer edge.
sector : a sector of a circle is a fraction of the interior of a circle. A sector is the part of a circle enclosed by two radii of a circle and their intercepted arc and; a sector is pie-shaped.
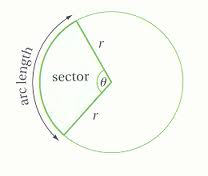 $A=\frac{x}{360}\pi r^{2}$
$A=\frac{x}{360}\pi r^{2}$
Reflection - critical questions regarding the teaching and learning of these benchmarks
- Do students understand the relationship between circumference and pi?
- Do students understand the relationship between circumference and diameter?
- Are students comfortable using the area formula for a circle?
- Are students accurate in their calculations and measurements?
- Are students able to find circumference if given radius?
- Are students able to find diameter given circumference?
- How are students using their knowledge of ratios and proportions to help them find areas of sectors?
- What is the relationship between the circumference and diameter of a circle?
- What does $\pi$ represent? How is it used to find circumference and area?
- How does changing the diameter of a circle affect its circumference?
Focus in Grade 7: Teaching with the curriculum focal points. NCTM, 2010. pg. 68.
Geometry word problem: The box problem and the goat problem.
http://www.purplemath.com/modules/perimetr5.htm
Minneapolis Public Schools Teacher created quiz to assess benchmark 7.3.1.2.
Minnesota Grade 7 Mathematics MCA-III Item Sampler Item, 2011, Benchmark 7.3.1.2
TAKS (Texas Assessment of Knowledge and Skills) Mathematics, Grade 8, 2010 released items.
Assessment
1.
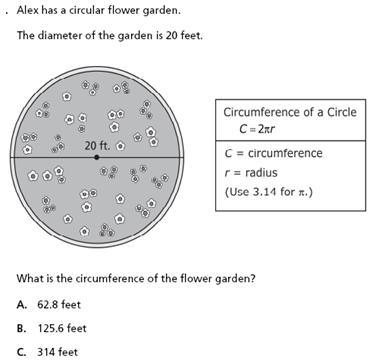
(Answer: A)
Minnesota Grade 7 Mathematics Modified MCA-III Item Sampler Item, 2011, Benchmark 7.3.1.1
2.
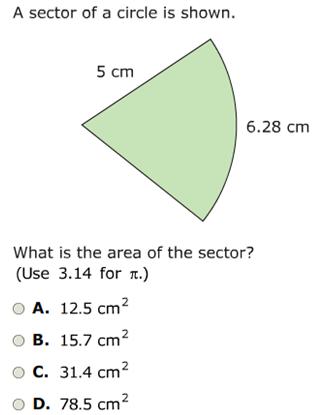
(answer: B)
Minnesota Grade 7 Mathematics MCA-III Item Sampler Item, 2011, Benchmark 7.3.1.1
3.
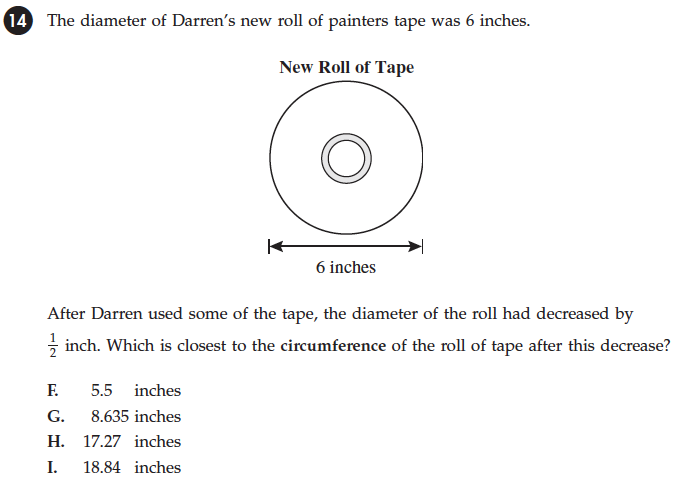
FCAT (Florida Comprehensive Assessment Test) Grade 7 released August 2006.
Correct answer: H
4.
The manager of a theater surveyed 500 people to determine their favorite type of play. Each person selected one type of play. The manager started to make the circle graph below to show the results of her survey.
Favorite Type of Play
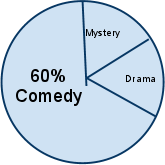
The percentage of people who selected drama was the same as the percentage
of people who selected mystery. Based on the information in the circle graph, what was the total number of people who selected drama?
A. 100
B. 125
C. 150
D. 200
5.
Linda bought a vegetarian pizza that was served on a metal tray. On the back of the tray, small letters stated that it has a circumference of 18.84 inches. What is the tray's radius?
Answer: approx. 3 inches
http://www.ixl.com/math/grade-7/circle-word-problems
(DOK Level 1)
6. Use the formula A = $\pi $r2to find the area of the circle. (Use $\frac{22}{7}$ for $\pi $).
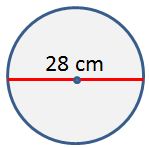
a) 44 cm2 b) 88 cm2 c) 616 cm2 d) 2464 cm2
Answer: c
(DOK Level 1)
7.
What is the circumference of the hockey puck? (Use 3.14 for $\pi $.)

Answer: 9.42 in.
DOK (Level 3)
8.
A circular sinkhole has a radius of 12 meters. A week later, it has a diameter of 48 meters. How much greater is the circumference of the sinkhole compared to the previous week? (Use 3.14 for $\pi $.)
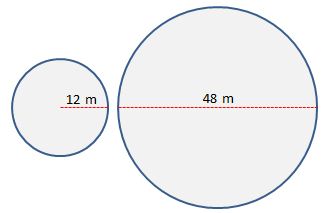
Answer: about 75.36 m (150.72 - 75.36)
(DOK Level 4)
9.
The figure is made up of a semicircle and a square. Find the perimeter. Use 3.14 for $\pi $. Explain how you found your answer.
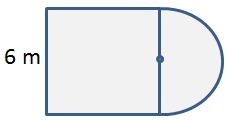
Sample Answer: The distance around the square is 6 + 6 + 6 = 18 meters. The distance around the curved part is one-half of the circumference of a circle with diameter = 6 meters.

Therefore, the perimeter of the figure is about 18 + 9.42 = 27.42 meters.
Differentiation
- Have students touch and trace with their fingers the circumference, radius and diameter of the circles/object used in class to reinforce the definitions of these terms. (kinesthetic)
- Trace over the radius and diameter; have students trace the circumference with a crayon onto paper.
- Provide area of circle formula.
- A mnemonic trick to remember the formula for circumference: C = π × d, is "cherry pie delight." Or 2πr = C is 2 pie are cherry (showing a picture of pies with 2 of them being cherry).
- A mnemonic trick to remember the formula for area of a circle, A = π × radius squared, is "apple pies are square." (Think of the apple pies that can be bought from McDonalds).
Using pictures that visually represent the definition of math vocabulary terms is particularly useful when working with geometric concepts. Below are examples for benchmark 7.3.1.1


- A mnemonic trick to remember the formula for circumference: C = π × d, is "cherry pie delight." Or 2πr = C is 2 pie are cherry (showing a picture of pies with 2 of them being cherry).
- A mnemonic trick to remember the formula for area of a circle, A = π × radius squared, is "apple pies are square." (Think of the apple pies that can be bought from McDonalds).
- A goat is tied to the corner of a 5-by-4-meter shed by an 8-meter piece of rope. Rounded to the nearest square meter, what is the area grazed by the goat?
What formula could they be expecting me to use for this? How on earth would I answer this? When in doubt, it can be helpful to draw a picture, so let's see what I can find:
The goat is tied at the upper right-hand corner with the dot. Now what? Well, on the nearest two sides, the goat can go this far:

This is three-quarters of a circle with radius 8 (the full length of the rope). The goat can walk around the far corners as far as the rope will allow. Along the top side, five meters of rope will be stretched along the side, leaving another three meters "in play;" along the right-hand side, four meters will have been used, leaving another four meters:

These new areas are both quarter-circles, one with radius 3 and the other with radius 4. There will be no way for the goat to reach the opposite corner or "overlap" in grazing, because he's out of rope. So these three partial circles mark off the total grazing area.
I know the formula for the area of a circle. To find, say, the area of $\frac{3}{4}$ of a circle, I'd just multiply the total area by $\frac{3}{4}$. So the total area is:
($\frac{3}{4}$)(pi)(82) + ($\frac{1}{4}$)(pi)(32) + ($\frac{1}{4}$)(pi)(42)
= 48pi + 2.25pi + 4pi = 54.25pi
I'm supposed to give my answer in terms of the nearest whole unit, so I'll plug the above into my calculator, and round.
The goat can graze about 170 square meters of grass.
Note how drawing the picture allowed me to "see" what I needed to do, immediately simplifying my work. If you have "no idea" what to do, try drawing a picture.
- Extension: Students can find out what percent of a circle is equivalent to how many degrees (not on standards, but a good extension activity/lesson).
- Have students make a circle with a specified circumference, without using a tape measure or a string (students work backward to find diameter or radius of circle)--have the students actually cut it out and then measure to see how close they are (use cm when measuring).
- Celebrating pi day can offer gifted students multiple ways to be creative, investigate interesting mathematics and apply their knowledge. There are many ideas for how to celebrate pi day on the web. Here are a few sites to start wtih: http://www.piday.org/ http://www.teachpi.org/ http://www.wikihow.com/Celebrate-Pi-Day . The book 'The Joy of Pi' by David Blatner is also a valuable resource.
- A lesson on the Golden ratio, although it is NOT dealing with circles, it refers to the ratios of geometric figures, similar to ratio of circumference to diameter is always pi, the Golden ratio of Rectangles says that the length to width ratio should be close to 1.6.
Golden Ratio: Also known as the divine proportion or golden mean, artists and architects have incorporated the golden ratio into their creations for centuries; many cultures consider it to be the most pleasing geometric proportion to the human eye. In this project, students measure the lengths and widths of common rectangles and discover that their ratio is close to the Golden Ratio. Have students measure and record the dimensions of an index card, a piece of notebook paper, a photograph, and other rectangular objects that can be found in the classroom. For each rectangle, students divide the length by the width. Most often the result of this division is a number close to 1.6, which is the golden ratio.
- (Read more: Fun Middle School Math Projects | eHow.com http://www.ehow.com/info_7856839_fun-middle-school-math-projects.html#ixzz1Oi3Cazgo)
Parents/Admin
Administrative/Peer Classroom Observation
|
Students are: |
Teachers are: |
|
measuring using correct units. |
circulating as the students do the 'vignette' activity, and be watching for errors. The values found should be close to 3.14, and if not, advise the students to measure again. |
|
entering values into their calculators and rounding correctly to get accurate values. |
guiding students on the use of protractors or angle rulers. |
|
using the correct formula to find circumference, not confusing it with the area formula. |
making sure students are using diameter vs. radius in appropriate situations. |
|
using angle rulers or protractors to make sectors of circles using degrees. |
making sure students have area as a squared units label, volume has a units cubed label, and length has a units label. |
|
using ratios, proportions, percents, and fractions. |
|
