4.3.2A Angles
Measure angles in geometric figures and real-world objects with a protractor or angle ruler.
Compare angles according to size. Classify angles as acute, right and obtuse.
For example: Compare different hockey sticks according to the angle between the blade and the shaft.
Overview
Standard 4.3.2 Essential Understandings
Fourth graders measure angles in real-world objects and geometric figures using protractors or angle rulers. They compare angles according to size and categorize angles as acute, right, or obtuse.
Fourth graders develop a conceptual understanding of area as they find the area of two dimensional figures by finding the total number of same-size square units that cover the shape without gaps or overlaps.
All Standard Benchmarks
4.3.2.1 Measure angles in geometric figures and real-world objects with a protractor or angle ruler.
4.3.2.2 Compare angles according to size. Classify angles as acute, right and obtuse.
4.3.2.3 Understand that the area of a two-dimensional figure can be found by counting the total number of same size square units that cover a shape without gaps or overlaps. Justify why length and width are multiplied to find the area of a rectangle by breaking the rectangle into one unit by one unit squares and viewing these as grouped into rows and columns.
4.3.2.4 Find the areas of geometric figures and real-world objects that can be divided into rectangular shapes. Use square units to label area measurements.
Benchmarks Group A
4.3.2.1 Measure angles in geometric figures and real-world objects with a protractor or angle ruler.
4.3.2.2 Compare angles according to size. Classify angles as acute, right and obtuse.
What students should know and be able to do [at a mastery level] related to these benchmarks:
- identify and classify angles as acute (less than 90 degrees)
- identify and classify angles as right (exactly 90 degrees) or
- identify and classify angles as obtuse (greater than 90 degrees)
- identify and classify real life examples of angles
For example: a window frame has 90 degree angles, the corners of a sports pennant are acute angles, a book lying open on a desk forms an obtuse angle, etc.
- use a protractor or angle ruler to accurately measure a given angle (within 3-5 degrees)
- compare and order angles based on their size- specifically angle measure
Work from previous grades that supports this new learning includes:
- Students have previously worked in building polygons based on the number of vertices's (corners or angles- depending on the language used by teachers) and sides it has. Based on these experiences, they have prior knowledge of the importance of angles in a shape.
NCTM Standards
Understand measurable attributes of objects and the units, systems, and processes of measurement.
Grades 3-5 Expectations:
- understand such attributes as length, area, weight, volume, and size of angle and select the appropriate type of unit for measuring each attribute;
- understand the need for measuring with standard units and become familiar with standard units in the customary and metric systems
- carry out simple unit conversions, such as from centimeters to meters, within a system of measurement;
- understand that measurements are approximations and how differences in units affect precision;
- explore what happens to measurements of a two-dimensional shape such as its perimeter and area when the shape is changed in some way.
Apply appropriate techniques, tools, and formulas to determine measurements.
Grades 3-5 Expectations:
- develop strategies for estimating the perimeters, areas, and volumes of irregular shapes;
- select and apply appropriate standard units and tools to measure length, area, volume, weight, time, temperature, and the size of angles;
- select and use benchmarks to estimate measurements;
- develop, understand, and use formulas to find the area of rectangles and related triangles and parallelograms;
- develop strategies to determine the surface areas and volumes of rectangular solids.
(NCTM, online measurement standards)
Common Core State Standards
Solve problems involving measurement and conversion of measurements from a larger unit to a smaller unit.
- 4.MD.1. Know relative sizes of measurement units within one system of units including km, m, cm; kg, g; lb, oz.; l, ml; hr, min, sec. Within a single system of measurement, express measurements in a larger unit in terms of a smaller unit. Record measurement equivalents in a two-column table. For example, know that 1 ft is 12 times as long as 1 in. Express the length of a 4 ft snake as 48 in. Generate a conversion table for feet and inches listing the number pairs (1, 12), (2, 24), (3, 36), ...
- 4.MD.2. Use the four operations to solve word problems involving distances, intervals of time, liquid volumes, masses of objects, and money, including problems involving simple fractions or decimals, and problems that require expressing measurements given in a larger unit in terms of a smaller unit. Represent measurement quantities using diagrams such as number line diagrams that feature a measurement scale.
- 4.MD.3. Apply the area and perimeter formulas for rectangles in real world and mathematical problems. For example, find the width of a rectangular room given the area of the flooring and the length, by viewing the area formula as a multiplication equation with an unknown factor.
Represent and interpret data.
- 4.MD.4. Make a line plot to display a data set of measurements in fractions of a unit (1/2, 1/4, 1/8). Solve problems involving addition and subtraction of fractions by using information presented in line plots. For example, from a line plot find and interpret the difference in length between the longest and shortest specimens in an insect collection.
Geometric measurement: Understand concepts of angle and measure angles.
- 4.MD.5. Recognize angles as geometric shapes that are formed wherever two rays share a common endpoint, and understand concepts of angle measurement:
- 4.MD.5a. An angle is measured with reference to a circle with its center at the common endpoint of the rays, by considering the fraction of the circular arc between the points where the two rays intersect the circle. An angle that turns through 1/360 of a circle is called a "one-degree angle," and can be used to measure angles.
- 4.MD.5b. An angle that turns through n one-degree angles is said to have an angle measure of n degrees.
- 4.MD.6. Measure angles in whole-number degrees using a protractor. Sketch angles of specified measure.
- 4.MD.7. Recognize angle measure as additive. When an angle is decomposed into non-overlapping parts, the angle measure of the whole is the sum of the angle measures of the parts. Solve addition and subtraction problems to find unknown angles on a diagram in real world and mathematical problems; e.g., by using an equation with a symbol for the unknown angle measure.
Misconceptions
Students may think...
- it is not important how they place the protractor prior to measuring an angle.
- angle size is dependent on the length of the rays
- the terms obtuse and acute are interchangeable
Resources
Teacher Notes
It is not important how they place the protractor on the angle before measuring.
Using a protractor is challenging work for fourth graders because for many of them it is the first time using the tool. It is important to teach the children to match up the "zero line" of the protractor with one side of the angle completely. They must also be sure to put the vertex in the exact middle of the protractor (below the 90∘ - there is usually a dot or a hole along the zero line) before measuring.
Because most protractors are designed to measure both left and right facing angles, two values are provided, one over the other (see picture below). Students are often confused by the two numbers present, not knowing which is the value of the angle. Teaching students to relate the number with the relative size, obtuse and acute, will help them accurately read the protractor.
For example: , an obtuse angle (one larger than 90o ) that points to both 125o and 55o when measured is understood to be 125o, because a 55o angle measure is associated with an acute angle (one smaller than 90o ).
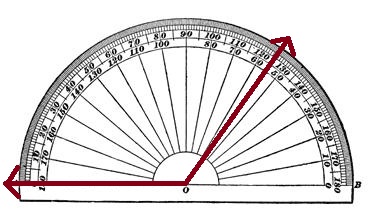
Make sure students have the opportunity to measure angles of a variety of sizes and orientations.
For example: angles that do not have one of the rays parallel to the bottom of the paper, angles that "open" both from the left and the right, angles that are smaller than the protractor-how do they solve the problem?
Students need to measure angles having sides of different lengths.
Students should measure the size of a given angle using an angle of know size.
Make a georule by connecting two strips of stiff paper 2" x 10" with a paper fastener. Use it to make different angles.
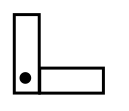
Once students have a clear understanding of acute angles (less than 90°), right angles (exactly 90°) and obtuse angles (more than 90°) they will be more accurate in measuring. When giving angles to measure, have students categorize it first (acute, obtuse, right) and then estimate a reasonable measurement.
For example: Given angle APC, first label it, then estimate the angle measure, then measure.
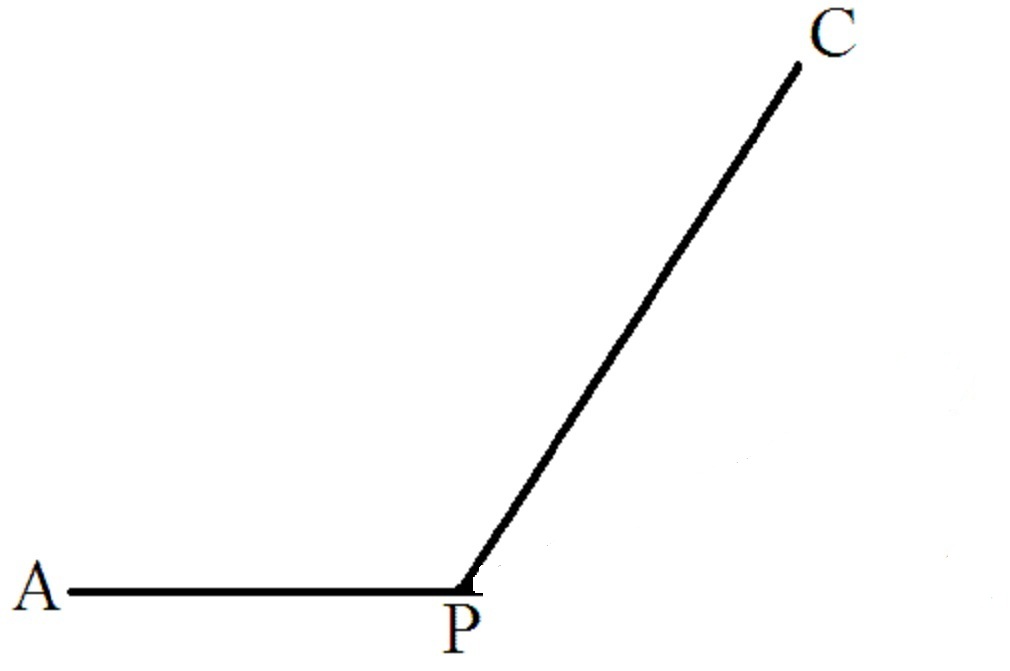 Angle APC is obtuse. Estimate is 110-115°. Actual is 120°
Angle APC is obtuse. Estimate is 110-115°. Actual is 120°
Now try it with angle CPD
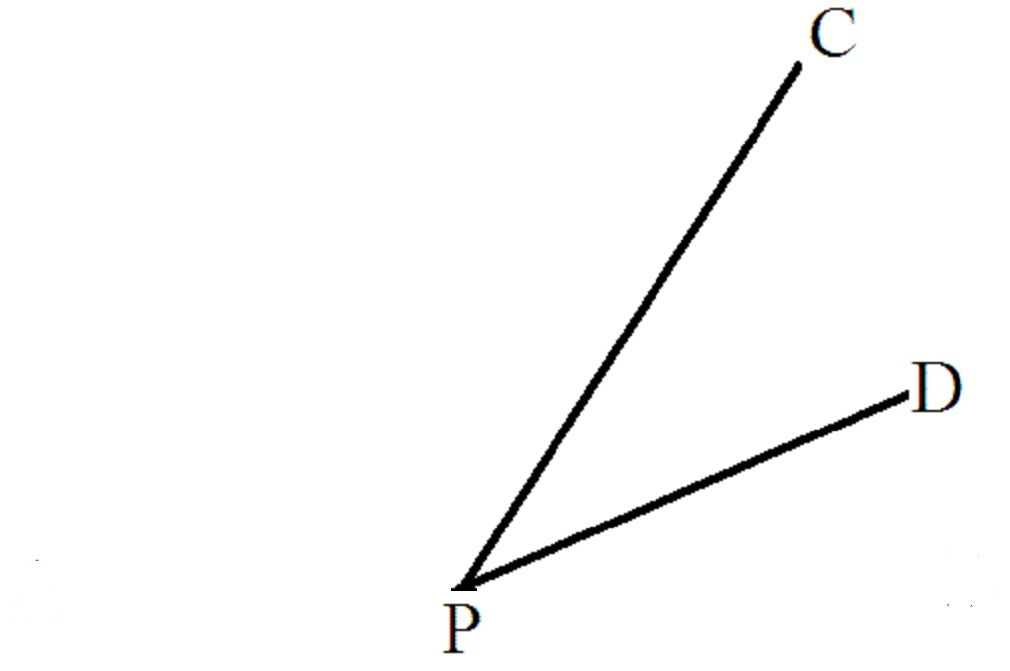 Angle CPD is acute. Estimate is 40°. Actual is 37°
Angle CPD is acute. Estimate is 40°. Actual is 37°
Questioning
Good questions, and good listening, will help children make sense of the mathematics, build self-confidence and encourage mathematical thinking and communication. A good question opens up a problem and supports different ways of thinking about it. The best questions are those that cannot be answered with a "yes" or a "no."
Getting Started
What do you need to find out?
What do you know now? How can you get the information? Where can you begin?
What terms do you understand/not understand?
What similar problems have you solved that would help?
While Working
How can you organize the information?
Can you make a drawing (model) to explain your thinking? What are other possibilities?
What would happen if...?
Can you describe an approach (strategy) you can use to solve this?
What do you need to do next?
Do you see any patterns or relationships that will help you solve this?
How does this relate to...?
Why did you...?
What assumptions are you making?
Reflecting about the Solution
How do you know your solution (conclusion) is reasonable? How did you arrive at your answer?
How can you convince me your answer makes sense?
What did you try that did not work? Has the question been answered?
Can the explanation be made clearer?
Responding (helps clarify and extend their thinking)
Tell me more.
Can you explain it in a different way?
Is there another possibility or strategy that would work?
Is there a more efficient strategy?
Help me understand this part ...
(Adapted from They're Counting on Us, California Mathematics Council, 1995)
NCTM Illuminations:
Lesson Name: Building With Triangles
Lesson Objectives:
- explore ways of building different basic shapes from triangles
- investigate basic properties of triangles
- investigate the relationships among basic geometrical shapes
- discover that it is not possible to construct some triangles from given lengths
- discover that the lengths of any two sides must be greater than the length of the third side
- build a foundation for the understanding of fractals
Other Instructional Resources:
*The following activity is from a website called mathplayground.com. It is a useful activity for helping students see and practice estimating a variety of angles.
Activity Name: Alien Angles
Activity Objective: The computer will generate an angle; students must estimate the angle within 5 degrees.
Additional Instructional Resources:
Anderson, N., Gavin, M., Dailey, J., Stone, W., & Vuolo, J. (2005). Navigating through measurement in grades 3-5. Reston, VA: National Council of Teachers of Mathematics.
Gavin, M., Belkin, L., Soinelli, A., & St. Marie, J. (2001). Navigating through geometry in grades 3-5. Reston, VA: National Council of Teachers of Mathematics.
Small, M. (2009). Good questions: Great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Van de Walle, J., Karp, K., Bay-Williams, J. (2010). Elementary and middle school mathematics: Teaching developmentally. (7th ed.). Boston, MA: Allyn & Bacon.
Van de Walle, J., & Lovin, L. (2006). Teaching student-centered mathematics grades 3-5. Boston, MA: Pearson Education.
"Vocabulary literally is the key tool for thinking."
Ruby Payne
New Vocabulary:
acute angle - an angle that measures more than 0° and less than 90°
obtuse angle - an angle that measures more than 90° and less than 180°
right angle - an angle that measures exactly 90°
protractor - an instrument used in measuring or drawing angles
Mathematics vocabulary words describe mathematical relationships and concepts and cannot be understood by simply practicing definitions. Students need to have experiences communicating ideas using these words to explain, support, and justify their thinking.
Learning vocabulary in the mathematics classroom is contingent upon the following:
Integration: Connecting new vocabulary to prior knowledge and previously learned vocabulary. The brain seeks connections and ways to make meaning which occurs when accessing prior knowledge.
Repetition: Using the word or concept many times during the learning process and connecting the word or concept with its meaning. The role of the teacher is to provide experiences that will guarantee connections are made between mathematical concepts, relationships, and corresponding vocabulary words.
Meaningful Use: Multiple and varied opportunities to use the words in context. These opportunities occur when students explain their thinking, ask clarifying questions, write about mathematics, and think aloud when solving problems. Teachers should be constantly probing student thinking in order to determine if students are connecting mathematics concepts and relationships with appropriate mathematics vocabulary.
Strategies for vocabulary development
Students do not learn vocabulary words by memorizing and practicing definitions. The following strategies keep vocabulary visible and accessible during instruction.
Mathematics Word Bank: Each unit of study should have word banks visible during instruction. Words and corresponding definitions are added to the word bank as the need arises. Students refer to word banks when communicating mathematical ideas which leads to greater understanding and application of words in context.
Labeled pictures and charts: Diagrams that are labeled provide opportunities for students to anchor their thinking as they develop conceptual understanding and increase opportunities for student learning.
Frayer Model: The Frayer Model connects words, definitions, examples and non-examples.
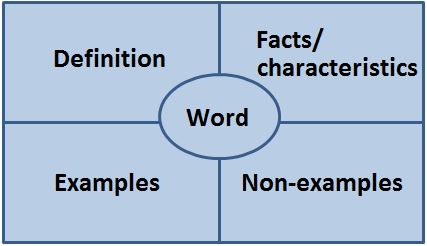
Example/Non-example Charts: This graphic organizer allows students to reason about mathematical relationships as they develop conceptual understanding of mathematics vocabulary words. Teachers should use these during the instructional process to engage student in thinking about the meaning of words.

Vocabulary Strips: Vocabulary strips give students a way to organize critical information about mathematics vocabulary words.
|
word |
definition |
illustration |
Encouraging students to verbalize thinking by drawing, talking, and writing, increases opportunities to use the mathematics vocabulary words in context.
Additional Resources for Vocabulary Development
Murray, M. (2004). Teaching mathematics vocabulary in context. Portsmouth, NH: Heinemann.
Sammons, L. (2011). Building mathematical comprehension: Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
What are the key ideas related to identifying and classifying angles at the fourth grade level? How do student misconceptions interfere with mastery of these ideas?
What experiences do students need in order to compare and classify angles?
What common errors do students make when identifying and classifying angles?
How can these errors be eliminated?
When checking for student understanding, what should teachers
- listen for in student conversations?
- look for in student work?
- ask during classroom discussions?
Examine student work related to a task involving the identification and classification of angles? What evidence do you need to say a student is proficient? Using three pieces of student work, determine what student understanding is observed through the work.
What are the key ideas related to understanding the measurement of angles at the fourth grade level? How do student misconceptions interfere with mastery of these ideas?
What experiences do students need in order to develop an understanding of the measurement of angles?
What tools should student use when measuring angles?
What common errors do students make when using a protractor?
How can these errors be avoided?
When checking for student understanding, what should teachers
- listen for in student conversations?
- look for in student work?
- ask during classroom discussions?
Examine student work related to a task involving the measurement of angles?
What evidence do you need to say a student is proficient? Using three pieces of student work, determine what student understanding is observed through the work.
How can teachers assess student learning related to these benchmarks?
How are these benchmarks related to other benchmarks at the fourth grade level?
Professional Learning Community Resources
Bamberger, H., Oberdorf, C., & Schultz-Ferrell, K. (2010). Math misconceptions prek-grade 5: From misunderstanding to deep understanding. Portsmouth, NH: Heinemann.
Chapin, S., and Johnson, A. (2006). Math matters: Understanding the math you teach, grades K-8. (2nd ed.). Sausalito, CA: Math Solutions Press.
Chapin, S., O'Connor, C., & Canavan Anderson, N. (2009). Classroom discussions: Using math talk to help students learn (Grades K-6). Sausalito, CA: Math Solutions.
Fosnot, C., & Dolk, M. (2002). Young mathematicians at work: Multiplication and division. Portsmouth, NH: Heinemann.
Hyde, Arthur. (2006). Comprehending math adapting reading strategies to teach mathematics, K-6. Portsmouth, NH: Heinemann.
Lester, F. (2010). Teaching and learning mathematics: Transforming research for elementary school teachers. Reston, VA: National Council of Teachers of Mathematics.
Otto, A., Caldwell, J., Wallus Hancock, S., & Zbiek, R.(2011). Developing essential understanding of multiplication and division for teaching mathematics in grades 3 - 5. Reston, VA.: National Council of Teachers of Mathematics.
Parrish, S. (2010). Number talks: Helping children build mental math and computation strategies grades K-5. Sausalito. CA: Math Solutions.
Sammons, L., (2011). Building mathematical comprehension: Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
Schielack, J. (2009). Focus in grade 3, teaching with curriculum focal points. Reston, VA: National Council of Teachers of Mathematics.
Bamberger, H., Oberdorf, C., & Schultz-Ferrell, K. (2010). Math misconceptions prek-grade 5: From misunderstanding to deep understanding. Portsmouth, NH: Heinemann.
Bender, W. (2009). Differentiating math instruction: Strategies that work for k-8 classrooms! Thousand Oaks, CA: Corwin Press.
Bresser, R., Melanese, K., & Sphar, C. (2008). Supporting English language learners in math class, grades k-2. Sausalito, CA: Math Solutions Publications.
Burns, Marilyn. (2007). About teaching mathematics: A k-8 resource (3rd ed.). Sausalito, CA: Math Solutions Publications.
Burns, M. (Ed). (1998). Leading the way: Principals and superintendents look at math instruction. Sausalito, CA: Math Solutions.
Caldera, C. (2005). Houghton Mifflin math and English language learners. Boston, MA: Houghton Mifflin Company.
Carpenter, T., Fennema, E., Franke, M., Levi, L., & Empson, S. (1999). Children's mathematics cognitively guided instruction. Portsmouth, NH: Heinemann.
Cavanagh, M. (2006). Math to learn: A mathematics handbook. Wilmington, MA: Great Source Education Group, Inc.
Chapin, S., & Johnson, A. (2006). Math matters: Understanding the math you teach, grades K-8. (2nd ed.). Sausalito, CA: Math Solutions Press.
Chapin, S., O'Connor, C., & Canavan Anderson, N. (2009). Classroom discussions: Using math talk to help students learn (Grades K-6). Sausalito, CA: Math Solutions.
Dacey, L., & Salemi, R. (2007). Math for all: Differentiating instruction k-2. Sausalito, CA: Math Solutions.
Donovan, S., & Bradford, J. (Eds). (2005). How students learn: Mathematics in the classroom. Washington, DC: National Academies Press.
Dougherty, B., Flores, A., Louis, E., & Sophian, C. (2010). Developing essential understanding of number & numeration pre-k-grade 2. Reston, VA: National Council of Teachers of Mathematics.
Felux, C., & Snowdy, P. (Eds.). ( 2006). The math coach field guide: Charting your course. Sausalito, CA: Math Solutions.
Fuson, K., Clements, D., & Beckmann, S. (2009). Focus in grade 2 teaching with curriculum focal points. Reston, VA: National Council of Teachers of Mathematics.
Hyde, Arthur. (2006). Comprehending math adapting reading strategies to teach mathematics, K-6. Portsmouth, NH: Heinemann.
Kilpatrick, J., & Swafford, J. (Eds). (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academies Press.
Leinwand, S. (2000). Sensible mathematics: A guide for school leaders. Portsmouth, NH: Heinemann.
Lester, F. (2010). Teaching and learning mathematics: Transforming research for elementary school teachers. Reston, VA: National Council of Teachers of Mathematics.
Murray, M. (2004). Teaching mathematics vocabulary in context. Portsmouth, NH: Heinemann.
Murray, M., & Jorgensen, J. (2007). The differentiated math classroom: A guide for teachers k-8. Portsmouth, NH: Heinemann.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: NCTM.
Parrish, S. (2010). Number talks: Helping children build mental math and computation strategies grades K-5. Sausalito. CA: Math Solutions.
Reeves, D. (2007). Ahead of the curve: The power of assessment to transform teaching and learning. Indiana: Solution Tree Press.
Sammons, L. (2011). Building mathematical comprehension: Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
Schielack, J., Charles, R., Clements, D., Duckett, P., Fennell, F., Lewandowski, S., ... & Zbiek, R. M. (2006). Curriculum focal points for prekindergarten through grade 8 mathematics: A quest for coherence. Reston, VA: NCTM.
Seeley, C. (2009). Faster isn't smarter: Messages about math teaching and learning in the 21st century. Sausalito, CA: Math Solutions.
Small, M. (2009). Good questions: Great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Van de Walle, J., Karp, K., Bay-Williams, J. (2010). Elementary and middle school mathematics: Teaching developmentally. (7th ed.). Boston, MA: Allyn & Bacon.
Van de Walle, J. A., & Lovin, L. H. (2006). Teaching student-centered mathematics grades K-3. Boston, MA: Pearson Education.
West, L., & Staub, F. (2003). Content focused coaching: Transforming mathematics lessons. Portsmouth, NH: Heinemann.
Assessment
- Using the protractor provided (protractor template can be photocopied onto an overhead transparency film), measure the angles of the triangle and label them.
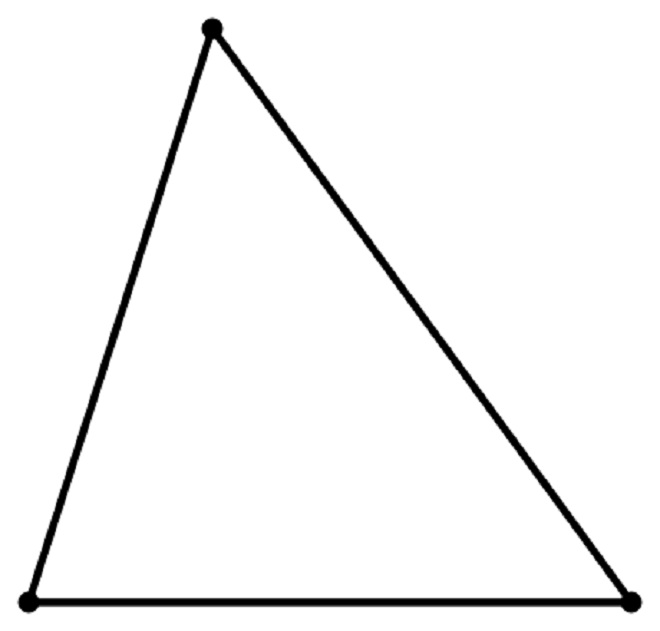
Solution: Accurate measures of angles
Benchmark: 4.3.2.1
- Look at each of the angles below.
Number them from 1-3 according to size, smallest to greatest.
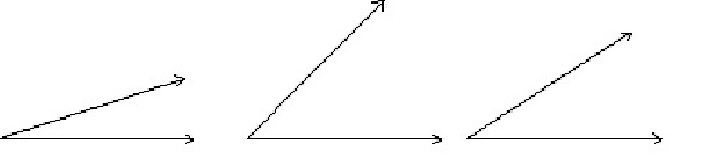
Solution: Correctly orders angles according to size.
Benchmark: 4.3.2.2
MCA III Item Sampler
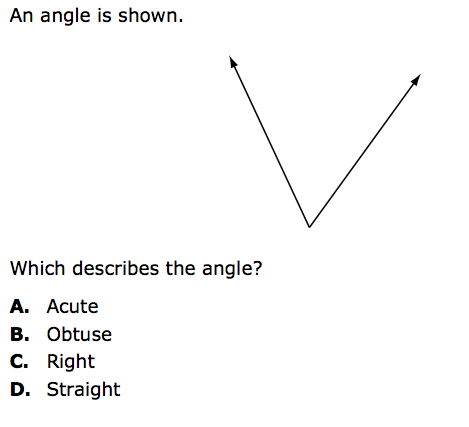
Solution: A. Acute
Benchmark: 4.3.2.2
MCA III Item Sampler
Differentiation
Students should compare angles to a right angle. Is it larger? Is it smaller? Using a right angle as a referent helps conceptual understanding of acute and obtuse angles.
Using the protractor is a skill that students may find challenging. As with any tool, repeated use over a long period of time is the best approach.
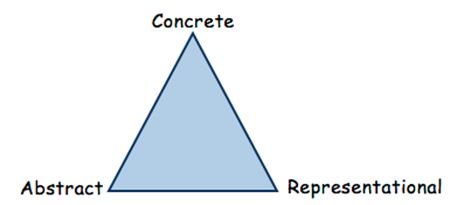
Concrete - Representational - Abstract Instructional Approach
The Concrete-Representational-Abstract Instructional Approach (CRA) is a research-based instructional strategy that has proven effective in enhancing the mathematics performance of students who struggle with mathematics.
The CRA approach is based on three stages during the learning process:
Concrete - Representational - Abstract
The Concrete Stage is the doing stage. The concrete stage is the most critical in terms of developing conceptual understanding of mathematical skills and concepts. At this stage, teachers use manipulatives to model mathematical concepts. The physical act of touching and moving manipulatives enables students to experience the mathematical concept at a concrete level. Research shows that students who use concrete materials develop more precise and comprehensive mental representations, understand and apply mathematical concepts, and are more motivated and on-task. Manipulatives must be selected based upon connections to the mathematical concept and the students' developmental level.
The Representational Stage is the drawing stage. Mathematical concepts are represented using pictures or drawings of the manipulatives previously used at the Concrete Stage. Students move to this level after they have successfully used concrete materials to demonstrate conceptual understanding and solve problems. They are moving from a concrete level of understanding toward an abstract level of understanding when drawing or using pictures to represent their thinking. Students continue exploring the mathematical concept at this level while teachers are asking questions to elicit student thinking and understanding.
The Abstract Stage is the symbolic stage. Teachers model mathematical concepts using numbers and mathematical symbols. Operation symbols are used to represent addition, subtraction, multiplication and division. Some students may not make a clean transfer to this level. They will work with some symbols and some pictures as they build abstract understanding. Moving to the abstract level too quickly causes many student errors. Practice at the abstract level will not lead to increased understanding unless students have a foundation based upon concrete and pictorial representations.
Additional Resources
Bender, W. (2009). Differentiating math instruction: Strategies that work for k-8 classrooms! Thousand Oaks, CA.: Corwin Press.
Dacey, L., & Lynch, J. (2007). Math for all: Differentiating instruction grades 3-5. Sausalito, CA: Math Solutions.
Murray, M. & Jorgensen, J. (2007). The differentiated math classroom: A guide for teachers k-8. Portsmouth, NH: Heinemann.
Small, M. (2009). Good questions: Great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Van de Walle, J., Karp, K., Bay-Williams, J. (2010). Elementary and middle school mathematics: Teaching developmentally. (7th ed.) Boston, MA: Allyn & Bacon.
Van de Walle, J. & Lovin, L. (2006). Teaching student-centered mathematics grades 3-5. Boston, MA: Pearson Education.
Protractor and degree are words that are new to ELL students. They may have used the words degree to measure or describe temperature. This is a new application of the term, however the symbol remain the same which can cause confusion. Since the protractor is a tool, this is an easier term to use. Once students understand the purpose for the protractor, the labeling with the symbol (°) makes more sense.
Students should compare angles to a right angle. Is it larger? Is it smaller? Using a right angle as a referent helps conceptual understanding of acute and obtuse angles. This also provides a context for applying appropriate terms.
- Word banks need to be part of the student learning environment in every mathematics unit of study. Refer to these throughout instruction.
- Word Use vocabulary graphic organizers such as the Frayer model (see below) to emphasize vocabulary words count, first, second, third, etc.

- Sentence Frames
Math sentence frames provide support that English Language Learners need in order to fully participate in math discussions. Sentence frames provide appropriate sentence structure models, increase the likelihood of responses using content vocabulary, help students to conceptualize words and build confidence in English Language Learners.
Sample sentence frames related to these benchmarks:
|
This is a/an _______________ angle because ______________________________. |
|
This angle is greater/less than this angle because ______________________________. |
- When assessing the math skills of an ELL student it is important to determine if the student has difficulty with the math concept or with the language used to describe the concept and conceptual understanding.
Additional ELL Resource
Bresser, R., Melanese, K., & Sphar, C. (2008). Supporting English language learners in math class, grades k-2. Sausalito, CA: Math Solutions Publications.
Engage students at a higher level by posing the following questions:
- For every triangle you measure, what is the sum of the angles? Why is that?
- What is the sum of the angles for all quadrilaterals? Why is that?
- What do you predict will be the sum of the angles of any given pentagon? Measure some examples. Where you accurate?
- What will help you to decide the sum of the interior angles of a shape with any given number of sides and angles?
Additional Resources
Bender, W. (2009). Differentiating math instruction: Strategies that work for k-8 classrooms!. Thousand Oaks, CA: Corwin Press.
Dacey, L., & Lynch, J. (2007). Math for all: Differentiating instruction grades 3-5. Sausalito, CA: Math Solutions.
Murray, M. & Jorgensen, J. (2007). The differentiated math classroom: A guide for teachers k-8. Portsmouth, NH: Heinemann.
Small, M. (2009). Good questions: Great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Parents/Admin
|
Students are... |
Teachers are... |
|
identifying angles as acute, right or obtuse in real life objects and geometric figures. |
providing real life and geometric figures for students to classify. |
|
using a protractor to measure angles accurately. |
assisting with proper protractor use. |
|
Given a set of angles: 1) identifying each angle as acute, right or obtuse; 2) accurately measuring each angle; 3) ordering the angles from smallest angle to greatest angle. |
providing a set of angles, feedback and assistance as needed. providing multiple opportunities for comparing angle size and measure. |
Additional Resources
For Mathematics Coaches
Chapin, S. and Johnson, A. (2006). Math matters: Understanding the math you teach: Grades k-8. (2nd ed.). Sausalito, CA: Math Solutions.
Donovan, S., & Bradford, J. (Eds). (2005). How students learn: Mathematics in the classroom. Washington, DC: National Academies Press.
Felux, C., & Snowdy, P. (Eds.). ( 2006). The math coach field guide: Charting your course. Sausalito, CA: Math Solutions.
Sammons, L., (2011). Building mathematical comprehension: Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
West, L., & Staub, F. (2003). Content focused coaching: Transforming mathematics lessons. Portsmouth, NH: Heinemann.
For Administrators
Burns, M. (Ed). (1998). Leading the way: Principals and superintendents look at math instruction. Sausalito, CA: Math Solutions.
Kilpatrick, J., & Swafford, J. (Eds). (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academies Press.
Leinwand, S. (2000). Sensible mathematics: A guide for school leaders. Portsmouth, NH: Heinemann.
Lester, F. (2010). Teaching and learning mathematics: Transforming research for school administrators. Reston, VA: National Council of Teachers of Mathematics.
Seeley, C. (2009). Faster isn't smarter: Messages about math teaching and learning in the 21st century. Sausalito, CA: Math Solutions.
Parent Resources
Mathematics handbooks to be used as home references:
Cavanagh, M. (2004). Math to Know: A mathematics handbook. Wilmington, MA: Great Source Education Group, Inc.
Cavanagh, M. (2006). Math to learn: A mathematics handbook. Wilmington, MA: Great Source Education Group, Inc.
Helping your child learn mathematics
Provides activities for children in preschool through grade 5
What should I look for in the mathematics program in my child's school? A Guide for Parents developed by SciMathMN
Help Your Children Make Sense of Math
Ask the right questions
In helping children learn, one goal is to assist children in becoming critical and independent thinkers. You can help by asking questions that guide, without telling them what to do.
Good questions, and good listening, will help children make sense of the mathematics, build self-confidence and encourage mathematical thinking and communication. A good question opens up a problem and supports different ways of thinking about it. The best questions are those that cannot be answered with a "yes" or a "no."
Getting Started
What do you need to find out?
What do you know now? How can you get the information? Where can you begin?
What terms do you understand/not understand?
What similar problems have you solved that would help?
While Working
How can you organize the information?
Can you make a drawing (model) to explain your thinking? What are other possibilities?
What would happen if . . . ?
Can you describe an approach (strategy) you can use to solve this?
What do you need to do next?
Do you see any patterns or relationships that will help you solve this?
How does this relate to ...?
Can you make a prediction?
Why did you...?
What assumptions are you making?
Reflecting about the Solution
How do you know your solution (conclusion) is reasonable? How did you arrive at your answer?
How can you convince me your answer makes sense?
What did you try that did not work?
Has the question been answered?
Can the explanation be made clearer?
Responding (helps clarify and extend their thinking)
Tell me more.
Can you explain it in a different way?
Is there another possibility or strategy that would work?
Is there a more efficient strategy?
Help me understand this part...
Adapted from They're counting on us, California Mathematics Council, 1995.
