2.3.3B Money
Identify pennies, nickels, dimes and quarters. Find the value of a group of coins and determine combinations of coins that equal a given amount.
For example: 50 cents can be made up of 2 quarters, or 4 dimes and 2 nickels, or many other combinations.
Overview

Standard 2.3.3 Essential Understandings
Second graders tell time to the quarter-hour and understand the difference between am and pm. They find the value of a group of coins including quarters, dimes, nickels and pennies. They find combinations of coins that equal a given amount.
All Standard Benchmarks
2.3.3.1
Tell time to the quarter-hour and distinguish between a.m. and p.m.
2.3.3.2
Identify pennies, nickels, dimes and quarters. Find the value of a group of coins and determine combinations of coins that equal a given amount.
Benchmark Group B
2.3.3.2
Identify pennies, nickels, dimes and quarters. Find the value of a group of coins and determine combinations of coins that equal a given amount.
What students should know and be able to do [at a mastery level] related to these benchmarks:
- identify and know the value of a quarter
- find the value of a group of quarters, dimes, nickels and pennies
- use quarters, dimes, nickels and pennies to show a given amount
- use the ¢ symbol properly
- skip by 25s
Work from previous grades that supports this new learning includes:
- identify and know the value of pennies, nickels and dimes;
- find the value (up to one dollar) of a group of dimes, nickels and pennies;
- count by fives to at least 100;
- count by tens to at least 100;
- count forward and backward by 10 from any two-digit number.
NCTM Standards
Understand measurable attributes of objects and the units, systems, and processes of measurement.
Pre-K - 2 Expectations
- recognize the attributes of length, volume, weight, area, and time;
- compare and order objects according to these attributes;
- understand how to measure using nonstandard and standard units;
- select an appropriate unit and tool for the attribute being measured.
Common Core State Standards
Work with time and money.
- 2.MD.7. Tell and write time from analog and digital clocks to the nearest five minutes, using a.m. and p.m.
- 2.MD.8. Solve word problems involving dollar bills, quarters, dimes, nickels, and pennies, using $ and ¢ symbols appropriately. Example: If you have 2 dimes and 3 pennies, how many cents do you have?
Misconceptions
Student Misconceptions and Common Errors
Students may think
- the value of a coin is related to its size; the larger the coin, the greater the value.
- a nickel is a quarter or vice versa.
- they count the coins rather than the value of the coins.
Vignette
In the Classroom
Ms. G wants her second graders to understand that a money amount can be represented in more than one way. Each child has a collection of coins: 6 quarters, 15 dimes, 10 nickels and 20 pennies.
Mrs. G. :Work with your partner to find three different ways make 28¢ with your coins. Record each combination in your math notebook.
As the children work, Ms. G. walks around the classroom monitoring the children's work, encouraging each group to find a combination that uses fewer/more coins than they had previously used.
Ms. G. asks children to share their coin combinations using a document camera.
Ms. G.: Ray, please come up and put your coins under the document camera.
Ray puts out one dime and eighteen pennies.

Ray - Ten, eleven, twelve, thirteen, . . . twenty eight.
Ms. G.: I noticed that you put the dime first and then counted on all the pennies. I'm glad you remembered to put the coin with the greatest value first. Ray, how did you write down the coins in your notebook?
Ray writes on the board- D, P, P, P, P, P, P, P, P, P, P, P, P, P, P, P, P, P, P.
Ms. G.: Corrine, please put up your coins.
Corrine puts out N, P, P, P, P, P, N, N, P, P, P, N
Corrine: five, six, seven, eight, nine, ten, um . . . fifteen, twenty, twenty-one, twenty-two, twenty-three, um . . . twenty-eight.
Ms. G.: Could you arrange your coins to make them easier to count?
Corrine: I could put all the nickels first.
Corrine rearranges the coins: N, N, N, N, P, P, P, P, P, P, P, P and the class counts 5, 10, 15, 20, 21, 22, 23, 24, 25, 26, 27, 28.
Ms. G.: Did anyone find a way to represent 28¢ that uses fewer coins?
Sher: I used dimes instead of all those nickels. D, D, P, P, P, P, P, P, P, P

The class counts the coins as Sher points to each.
Ms. G.: Thanks, Sher. Is there a way to show 28¢ with fewer coins?
Kylie: I used six coins.
Ms. G.: Bring them up.
Kylie puts out D, D, N, P, P, P.

Ms. G.: Kylie, please point while we count.
Students: Ten, twenty, twenty-five, twenty-six, twenty-seven, twenty-eight.
Ms. G.: Can we do it with fewer coins?
Kyra: I used a quarter, and three pennies.
Q, P, P, P

Ms. G.: Let's count them together:
Students: twenty-five, twenty-six, twenty-seven, twenty-eight
Ms. G.: Have we shown all the ways to make twenty-eight cents?
Kyra: I think there are more ways but how do you know when you've got them all?
Ms. G.: That's a good question. Any ideas?
Emma: We could make a list.
Ms. G.: Tell me more . . .
Emma: We could make a table and start listing all the ways.
Ms. G.: Okay, come on up and draw a table.

Ms. G.: What do the labels of your columns mean?
Emma: Q is for quarters, D is for dimes, N is for nickels, P is for pennies.
Ms. G.: What will record in the table?
Josiah: The number of each coin we use.
Ms. B: Good idea. Do you want to start with the fewest possible coins or the
most coins?
Ms. B. wants to start with either the most or the fewest coins in order to generate an organized list to help them keep track of all the combinations.
Ray: Let's start with all pennies.
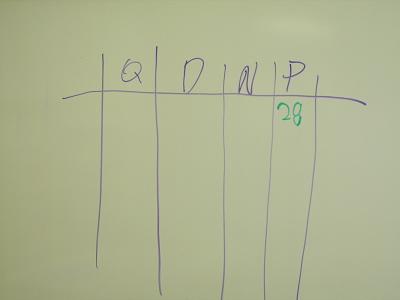
Ms. G.: Okay, if we're going to make an "organized" list, where do we go next?
Sami: Well, pennies are the smallest coins, and nickels are the next, so we can change 5 pennies for a nickel.

As exchanges are made the new coin combination is recorded on the chart.
Ms. G.: What's next? Jason?
Jason: Change another 5 pennies for another nickel.

Ms. G.: I would like everyone to make this table in their math notebooks. Be sure to make four columns, one for each coin. Then put in the information we have written so far. Be sure to put it in the correct order, starting with the 28 pennies first.
Who would like to come up and put in the next combinations of coins?
April: Change another 5 pennies for a nickel. Now we have 3 nickels and 13 pennies.

Jeremiah: Use another nickel. Then it's four nickels and 8 pennies.

Kahlim: We can use five nickels and 3 pennies.

Ms. G.: What patterns do you notice in the numbers in our chart?
Will: The number in the nickels column goes up by one every time.
Maya : The number of pennies goes down five.
Ms. G.: Why would those patterns appear?
Maya: Well, we are using one more nickel each time, so that's why it goes up by one.
Kahlim: And we have to trade 5 pennies for the nickels every time, so that is going down by five.
Ms. G.: Nice explanation. What's next?
Daida: We can use dimes.
Ms. G.: If we use one dime, how many pennies would we need to make 28¢?
Daida: One dime and 18 pennies.
Will: Then we can trade for nickels again. One dime, one nickel, and 13 pennies.
Kyra: One dime, two nickels, and 8 pennies.
Jose: Put in another nickel and then 3 pennies.
Emma: Look - the pattern in the nickels and pennies is kinda the same!
Ms. G.: Why would that happen?
Kahlim: For the same reason - every time we use another nickel the nickels go up by 1 and the pennies go down by 5.
Kyra: Can we use 2 dimes now?
Ms. G.: Come on up and fill in the chart.
Daida: Next we trade five pennies for a nickel!
Jose: There's only one way left.
Ms. G.; How do you know?
Jose: The only thing left is to use a quarter. We can't use more than 2 dimes and one nickel.
Ms. G.: Good thinking. Come on up and write it on the chart.

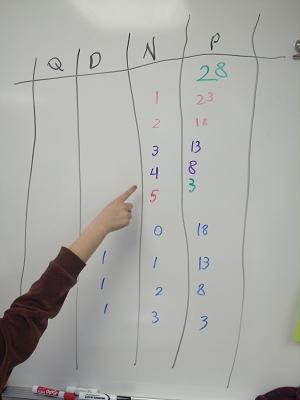
Ms. G.: Let's look at our chart. What patterns do you see?
Ray: The pennies only has eights and threes.

Ms. G.: Why would that happen?
Jose: Because the difference between eight and three is five, so every time we take away a nickel it changes between 3 and 8.
Kyra: There's a pattern in the nickels, too.
Ms. G.: Describe it . . .
Kyra: It goes up by one. The first time it went all the way up to 5. After we used a dime, it only went up to 3. Then with two dimes it was only 0 and 1.
Ms. G.: Why would that happen?
Kyra: Well, I think it has something to do with using dimes - but I can't figure it out.
Ms. G.: What do you know about the relationship between dimes and nickels?
Kyra: I know that two nickels make a dime.
Ms. G.: So if we use dimes to make our 28¢, what will happen to the
number of nickels?
Kyra: It will go down.
Ms. G.: How much?
Kyra: The nickels will go down by 2 every time we use a dime.
Ms. G.: So, if we use any dimes, what does that do to the highest number of nickels we can use.
Kyra: It will be two smaller - Oh, so that's why it [the number of nickels] will only go up to three when we use dimes!
Ms. G.: Good question and good thinking to figure it out - I'm proud of you, Kyra!
Daida: I see another pattern - in the dimes!
Ms. G.: Describe the pattern.
Daida: It goes 1, 1, 1, 1, 2, 2.

Ms. G.: Why does "1" appear four times and "2" only appears twice?

Daida: Because there are more ways to use one dime - 'cause we can have a dime with no nickels, one nickel, two nickels, or three nickels.
Ms. G.: Nice explanation.
Ray: Wow - there are thirteen different ways to show 28¢!
Ms. G. is confident that her second graders realize there can be many ways to represent a given money amount using coins.
Resources
Teacher Notes
- Students may need support in further development of previously studied concepts and skills.
- Coins can be counted in any order. Students often group coins by size and begin the count with the coin having the greatest value. Other efficient strategies could also be used.
- As students count groups of coins, give a signal to indicate a new skip counting amount. For example, 25 (Q), 50 (Q) clap, 60 (D), 70 (D) clap, 75 (N), clap, 76 (P), 77 (P), 78 (P).
- Students may have a hard time skip counting by 25s. Create a counting by 25 chart and refer to it when finding the value of a group of quarters.
- Questioning
Good questions, and good listening, will help children make sense of the mathematics, build self-confidence and encourage mathematical thinking and communication. A good question opens up a problem and supports different ways of thinking about it. The best questions are those that cannot be answered with a "yes" or a "no."
Getting Started
What do you need to find out?
What do you know now? How can you get the information? Where can you begin?
What terms do you understand/not understand?
What similar problems have you solved that would help?
While Working
How can you organize the information?
Can you make a drawing (model) to explain your thinking? What are other possibilities?
What would happen if...?
Can you describe an approach (strategy) you can use to solve this?
What do you need to do next?
Do you see any patterns or relationships that will help you solve this?
How does this relate to...?
Why did you...?
What assumptions are you making?
Reflecting about the Solution
How do you know your solution (conclusion) is reasonable? How did you arrive at your answer?
How can you convince me your answer makes sense?
What did you try that did not work? Has the question been answered?
Can the explanation be made clearer?
Responding (helps clarify and extend their thinking)
Tell me more.
Can you explain it in a different way?
Is there another possibility or strategy that would work?
Is there a more efficient strategy?
Help me understand this part ...
(Adapted from They're Counting on Us, California Mathematics Council, 1995)
NCTM Illuminations
- Number Cents In this unit, students explore the relationship between pennies, nickels, dimes, and quarters. They count sets of mixed coins, write story problems that involve money, and use coins to make patterns. The unit consists of six lessons that give children an opportunity to identify individual coins and to make sets of coins with equivalent values. They also pattern with coins and use coins in real world situations. They will also determine the value of sets of pennies, nickels, dimes, and quarters and record the value using 2 forms of notation. Actual coins are used in all lessons. Numerous connections to children's literature are made in this unit. Suggestions for books dealing with money and coins are available.
- Coin Box Students count and exchange coins.
- Primary Economics In this lesson, students will play the role of a consumer as they learn how to use different combinations of coins to make money amounts up to 25 cents. Students will earn money and save it in their piggy banks until they have the exact amount to purchase an item of their choice.
MATH LEARNING CENTER
Additional Instructional Resources
Small, M. (2009). Good questions: Great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Van de Walle, J., Karp, K., Bay-Williams, J. (2010). Elementary and middle school mathematics: Teaching developmentally. (7th ed.) . Boston, MA: Allyn & Bacon.
Van de Walle, J. & Lovin, L. (2006). Teaching student-centered mathematics grades k-3. Boston, MA: Pearson Education.
cent sign - The sign used to show cents (¢).
quarter - A coin that has a value of 25¢.
"Vocabulary literally is the
key tool for thinking."
Ruby Payne
Mathematics vocabulary words describe mathematical relationships and concepts and cannot be understood by simply practicing definitions. Students need to have experiences communicating ideas using these words to explain, support, and justify their thinking.
Learning vocabulary in the mathematics classroom is contingent upon the following:
Integration: Connecting new vocabulary to prior knowledge and previously learned vocabulary. The brain seeks connections and ways to make meaning which occurs when accessing prior knowledge.
Repetition: Using the word or concept many times during the learning process and connecting the word or concept with its meaning. The role of the teacher is to provide experiences that will guarantee connections are made between mathematical concepts, relationships, and corresponding vocabulary words.
Meaningful Use: Multiple and varied opportunities to use the words in context. These opportunities occur when students explain their thinking, ask clarifying questions, write about mathematics, and think aloud when solving problems. Teachers should be constantly probing student thinking in order to determine if students are connecting mathematics concepts and relationships with appropriate mathematics vocabulary.
Strategies for vocabulary development
Students do not learn vocabulary words by memorizing and practicing definitions. The following strategies keep vocabulary visible and accessible during instruction.
Mathematics Word Bank: Each unit of study should have word banks visible during instruction. Words and corresponding definitions are added to the word bank as the need arises. Students refer to word banks when communicating mathematical ideas which leads to greater understanding and application of words in context.
Labeled pictures and charts: Diagrams that are labeled provide opportunities for students to anchor their thinking as they develop conceptual understanding and increase opportunities for student learning.
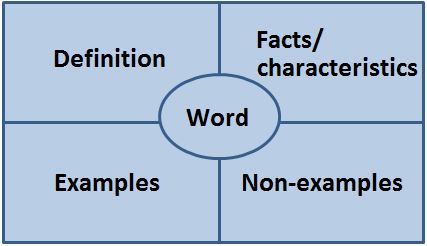
Frayer Model: The Frayer Model connects words, definitions, examples and non-examples.
Example/Non-example Charts: This graphic organizer allows students to reason about mathematical relationships as they develop conceptual understanding of mathematics vocabulary words. Teachers should use these during the instructional process to engage student in thinking about the meaning of words.

Vocabulary Strips: Vocabulary strips give students a way to organize critical information about mathematics vocabulary words.
|
word |
definition |
illustration |
Encouraging students to verbalize thinking by drawing, talking, and writing increases opportunities to use the mathematics vocabulary words in context.
Additional Resources for Vocabulary Development
Murray, M. (2004). Teaching mathematics vocabulary in context. Portsmouth, NH: Heinemann.
Sammons, L. (2011). Building mathematical comprehension: Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
What are the key ideas related to identifying and counting a group of coins (pennies, nickels, dimes and quarters) at the second grade level? How do student misconceptions interfere with mastery of these ideas?
What experiences do students need in order to identify and count a group of coins (pennies, nickels, dimes and quarters) successfully?
What common errors do second graders make when counting groups of coins?
When checking for student understanding of coin counting at the second grade level, what should teachers
- listen for in student conversations?
- look for in student work?
- ask during classroom discussions?
Examine student work related to a task involving counting a group of coins (pennies, nickels, dimes and quarters). What evidence do you need to say a student is proficient? Using three pieces of student work, determine what student understanding is observed through the work.
How can teachers assess student learning related to these benchmarks?
How are these benchmarks related to other benchmarks at the second grade level?
Materials for PLC
Bamberger, H., Oberdorf, C., & Schultz-Ferrell, K.. (2010). Math misconceptions prek-grade 5: From misunderstanding to deep understanding. Portsmouth, NH: Heinemann.
Chapin, S. and Johnson, A. (2006). Math matters, understanding the math you teach, grades K-8. (2nd. ed.). Sausalito, CA: Math Solutions Press.
Chapin, S., O'Connor, C., & Canavan Anderson, N. (2009). Classroom discussions: Using math talk to help students learn (Grades K-6). Sausalito, CA: Math Solutions.
Hyde, Arthur. (2006) Comprehending math adapting reading strategies to teach mathematics, K-6. Portsmouth, NH: Heinemann.
Lester, F. (2010). Teaching and learning mathematics: Transforming research for elementary school teachers. Reston, VA: National Council of Teachers of Mathematics.
Sammons, L., (2011). Building mathematical comprehension. Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
Bamberger, H., Oberdorf, C., & Schultz-Ferrell, K. (2010). Math misconceptions prek-grade 5: From misunderstanding to deep understanding. Portsmouth, NH: Heinemann.
Bender, W. (2009). Differentiating math instruction: Strategies that work for k-8 classrooms! Thousand Oaks, CA: Corwin Press.
Bresser, R., Melanese, K., & Sphar, C. (2008). Supporting English language learners in math class, grades k-2. Sausalito, CA: Math Solutions Publications.
Burns, Marilyn. (2007). About teaching mathematics: A k-8 resource (3rd ed.). Sausalito, CA: Math Solutions Publications.
Burns, M. (Ed). (1998). Leading the way: Principals and superintendents look at math instruction. Sausalito, CA: Math Solutions.
Caldera, C. (2005). Houghton Mifflin math and English language learners. Boston, MA: Houghton Mifflin Company.
Carpenter, T., Fennema, E., Franke, M., Levi, L., & Empson, S. (1999). Children's mathematics cognitively guided instruction. Portsmouth, NH: Heinemann.
Cavanagh, M. (2006). Math to learn: A mathematics handbook. Wilmington, MA: Great Source Education Group, Inc.
Chapin, S., & Johnson, A. (2006). Math matters: Understanding the math you teach, grades K-8. (2nd ed.). Sausalito, CA: Math Solutions Press.
Chapin, S., O'Connor, C., & Canavan Anderson, N. (2009). Classroom discussions: Using math talk to help students learn (Grades K-6). Sausalito, CA: Math Solutions.
Dacey, L., & Salemi, R. (2007). Math for all: Differentiating instruction k-2. Sausalito, CA: Math Solutions.
Donovan, S., & Bradford, J. (Eds). (2005). How students learn: Mathematics in the classroom. Washington, DC: National Academies Press.
Dougherty, B., Flores, A., Louis, E., & Sophian, C. (2010). Developing essential understanding of number & numeration pre-k-grade 2. Reston, VA: National Council of Teachers of Mathematics.
Felux, C., & Snowdy, P. (Eds.). ( 2006). The math coach field guide: Charting your course. Sausalito, CA: Math Solutions.
Fuson, K., Clements, D., & Beckmann, S. (2009). Focus in grade 2 teaching with curriculum focal points. Reston, VA: National Council of Teachers of Mathematics.
Hyde, Arthur. (2006). Comprehending math adapting reading strategies to teach mathematics, K-6. Portsmouth, NH: Heinemann.
Kilpatrick, J., & Swafford, J. (Eds). (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academies Press.
Leinwand, S. (2000). Sensible mathematics: A guide for school leaders. Portsmouth, NH: Heinemann.
Lester, F. (2010). Teaching and learning mathematics: Transforming research for elementary school teachers. Reston, VA: National Council of Teachers of Mathematics.
Murray, M. (2004). Teaching mathematics vocabulary in context. Portsmouth, NH: Heinemann.
Murray, M., & Jorgensen, J. (2007). The differentiated math classroom: A guide for teachers k-8. Portsmouth, NH: Heinemann.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: NCTM.
Parrish, S. (2010). Number talks: Helping children build mental math and computation strategies grades K-5. Sausalito. CA: Math Solutions.
Sammons, L. (2011). Building mathematical comprehension: Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
Schielack, J., Charles, R., Clements, D., Duckett, P., Fennell, F., Lewandowski, S., ... & Zbiek, R. M. (2006). Curriculum focal points for prekindergarten through grade 8 mathematics: A quest for coherence. Reston, VA: NCTM.
Seeley, C. (2009). Faster isn't smarter: Messages about math teaching and learning in the 21st century. Sausalito, CA: Math Solutions.
Small, M. (2009). Good questions: Great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Van de Walle, J., Karp, K., Bay-Williams, J. (2010). Elementary and middle school mathematics: Teaching developmentally. (7th ed.). Boston, MA: Allyn & Bacon.
Van de Walle, J. A., & Lovin, L. H. (2006). Teaching student-centered mathematics grades K-3. Boston, MA: Pearson Education.
West, L., & Staub, F. (2003). Content focused coaching: Transforming mathematics lessons. Portsmouth, NH: Heinemann.
Assessment
- Taylor buys a candy bar. He spends the coins shown. How much does the candy bar cost?





Solution: 90¢
Benchmark: 2.3.3.2
- Becca has these coins.
What is the total value of her coins?






Solution: 56¢
Benchmark: 2.3.3.2
- Which shows 35¢?
A.


B.




C.


D.



Solution: C.
Benchmark: 2.3.3.2
- Brian draws 2 quarters and 2 dimes to show 70¢.
Show 70¢ in a different way. Draw and label each coin.
Solution: The drawing must show labeled coins with a value of 70¢ in a different way. For example, 7 dimes or 2 quarters and 4 nickels.
Benchmark: 2.3.3.2
- What is the total value of these coins?




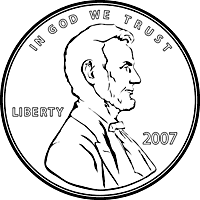


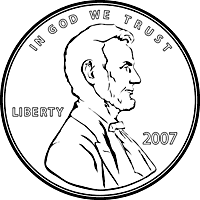
Solution: 69¢
Benchmark: 2.3.3.2
Differentiation
- Using models that represent the composite coins with pennies gives support to students who are still counting by 1s or need support in exchanging pennies for nickels or dimes.


Skip counting coins of the same value will help students build their understanding of counting coins. For example, when finding the value of dimes, they can skip count by 10s: 10¢, 20¢, 30¢, 40¢, 50¢. When finding the value of a set of nickels, they can skip count by 5s: 5¢, 10¢, 15¢, 20¢, 25¢, 30¢, 35¢, 40¢, 45¢. Incorporate skip counting practice for each coin, then try a mix of two coins in a set to build on their skip counting skills. Display coins, such as: dime, dime, dime, nickel, nickel and invite students to count on as they touch each coin: 10, 20, 30. . . when the coin type changes from dimes to nickels, pause. Have students put up their fingers to show the value of the next coin (raise five fingers) and note that they will now skip count by 5s. . . 35, 40.
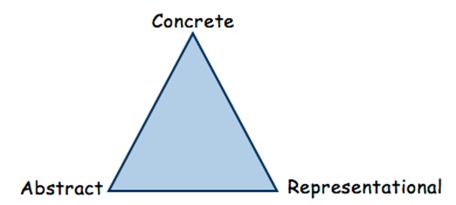
Concrete - Representational - Abstract Instructional Approach
The Concrete-Representational-Abstract Instructional Approach (CRA) is a research-based instructional strategy that has proven effective in enhancing the mathematics performance of students who struggle with mathematics.
The CRA approach is based on three stages during the learning process:
Concrete - Representational - Abstract
The Concrete Stage is the doing stage. The concrete stage is the most critical in terms of developing conceptual understanding of mathematical skills and concepts. At this stage, teachers use manipulatives to model mathematical concepts. The physical act of touching and moving manipulatives enables students to experience the mathematical concept at a concrete level. Research shows that students who use concrete materials develop more precise and comprehensive mental representations, understand and apply mathematical concepts, and are more motivated and on-task. Manipulatives must be selected based upon connections to the mathematical concept and the students' developmental level.
The Representational Stage is the drawing stage. Mathematical concepts are represented using pictures or drawings of the manipulatives previously used at the Concrete Stage. Students move to this level after they have successfully used concrete materials to demonstrate conceptual understanding and solve problems. They are moving from a concrete level of understanding toward an abstract level of understanding when drawing or using pictures to represent their thinking. Students continue exploring the mathematical concept at this level while teachers are asking questions to elicit student thinking and understanding.
The Abstract Stage is the symbolic stage. Teachers model mathematical concepts using numbers and mathematical symbols. Operation symbols are used to represent addition, subtraction, multiplication and division. Some students may not make a clean transfer to this level. They will work with some symbols and some pictures as they build abstract understanding. Moving to the abstract level too quickly causes many student errors. Practice at the abstract level will not lead to increased understanding unless students have a foundation based upon concrete and pictorial representations.
Additional Resources
Bender, W. (2009). Differentiating math instruction: Strategies that work for k-8 classrooms! Thousand Oaks, CA.: Corwin Press.
Dacey, L., & Lynch, J. (2007). Math for all: Differentiating instruction grades k-2 Sausalito, CA: Math Solutions.
Murray, M. & Jorgensen, J. (2007). The differentiated math classroom: A guide for teachers k-8. Portsmouth, NH: Heinemann.
Small, M. (2009). Good questions: Great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Van de Walle, J., Karp, K., Bay-Williams, J. (2010). Elementary and middle school mathematics: Teaching developmentally. (7th ed.). Boston, MA: Allyn & Bacon.
Van de Walle, J. & Lovin, L. (2006). Teaching student-centered mathematics grades k-3. Boston, MA: Pearson Education.
Students may recognize the difference between coins but not be able to use correct vocabulary in naming them. Labeled pictures provide a reference.
Understanding the value of a coin can be challenging since the value of one cannot be "built" from another even though they are related in value. Again, a chart that indicates the relationship between coins will provide immediate access for students.
The different names and representations for the same amount can be confusing, for example, 25¢, a "quarter," $0.25, "quarter of a dollar," and 25 cents.
If students are familiar with pesos and centavos, connect the words to dollars and cents. 1 dollar = 100 cents, 1 peso = 100 centavos. The value of a peso is about the same as a dime.
- Word banks need to be part of the student learning environment in every mathematics unit of study. Refer to these throughout instruction.
- Use vocabulary graphic organizers such as the Frayer model (see below) to emphasize vocabulary words such as quarter, cents.

- Sentence Frames
Math sentence frames provide support that English Language Learners need in order to fully participate in math discussions. Sentence frames provide appropriate sentence structure models, increase the likelihood of responses using content vocabulary, help students to conceptualize words and build confidence in English Language Learners.
Sample sentence frames related to these benchmarks:
|
This is a ________________________. It is worth ______________________________. |
|
When I count ____________ I count by ____________________. |
- When assessing the math skills of an ELL student it is important to determine if the student has difficulty with the math concept or with the language used to describe the concept and conceptual understanding.
Additional ELL Resources:
Bresser, R., Melanese, K., & Sphar, C. (2008). Supporting English language learners in math class, grades k-2. Sausalito, CA: Math Solutions Publications.
Students show a given amount in more than three ways.
Students investigate coins from countries around the world and their values.
Investigating state quarters might intrigue students. The United States Mint made state quarters between 1999 and 2008.
Additional Resources
Bender, W. (2009). Differentiating math instruction: Strategies that work for k-8 classrooms! Thousand Oaks, CA.: Corwin Press.
Dacey, L., & Lynch, J. (2007). Math for all: Differentiating instruction grades k-2. Sausalito, CA: Math Solutions.
Murray, M., & Jorgensen, J. (2007). The differentiated math classroom: A guide for teachers k-8. Portsmouth, NH: Heinemann.
Small, M. (2009). Good questions: Great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Parents/Admin
Administrative/Peer Classroom Observation
|
Students are ... |
Teachers are... |
|
counting groups of quarters, dimes, nickels and pennies. |
providing opportunities to solve real-world problems involving money. |
|
using quarters, dimes, nickels and pennies to show a given amount in more than one way. |
keeping the relationship between coins visible in the classroom.
|
|
using quarters, dimes, nickels and pennies to show a given amount using the fewest coins. |
|
Additional Resources
For Mathematics Coaches
Chapin, S. and Johnson, A. (2006). Math matters: Understanding the math you teach: Grades k-8, 2nd edition. Sausalito, CA: Math Solutions.
Donovan, S., & Bradford, J. (Eds). (2005). How students learn: Mathematics in the classroom. Washington, DC: National Academies Press.
Felux, C., & Snowdy, P. (Eds.). ( 2006). The math coach field guide: Charting your course. Sausalito, CA: Math Solutions.
Sammons, L., (2011). Building mathematical comprehension: Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
West, L., & Staub, F. (2003). Content focused coaching: Transforming mathematics lessons. Portsmouth, NH: Heinemann.
For Administrators
Burns, M. (Ed). (1998). Leading the way: Principals and superintendents look at math instruction. Sausalito, CA: Math Solutions.
Kilpatrick, J., & Swafford, J. (Eds). (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academies Press.
Leinwand, S. (2000). Sensible mathematics: A guide for school leaders. Portsmouth, NH: Heinemann.
Lester, F. (2010). Teaching and learning mathematics: Transforming research for school administrators. Reston, VA: National Council of Teachers of Mathematics.
Seeley, C. (2009). Faster isn't smarter: Messages about math teaching and learning in the 21st century. Sausalito, CA: Math Solutions.
Mathematics handbooks to be used as home references:
Cavanagh, M. (2004). Math to Know: A mathematics handbook. Wilmington, MA: Great Source Education Group, Inc.
Cavanagh, M. (2006). Math to learn: A mathematics handbook. Wilmington, MA: Great Source Education Group, Inc.
Helping your child learn mathematics Provides activities for children in preschool through grade 5
What should I look for in the mathematics program in my child's school? A Guide for Parents developed by SciMathMN
Help Your Children Make Sense of Math
Ask the right questions
In helping children learn, one goal is to assist children in becoming critical and independent thinkers. You can help by asking questions that guide, without telling them what to do.
Good questions, and good listening, will help children make sense of the mathematics, build self-confidence and encourage mathematical thinking and communication. A good question opens up a problem and supports different ways of thinking about it. The best questions are those that cannot be answered with a "yes" or a "no."
Getting Started
What do you need to find out?
What do you know now? How can you get the information? Where can you begin?
What terms do you understand/not understand?
What similar problems have you solved that would help?
While Working
How can you organize the information?
Can you make a drawing (model) to explain your thinking? What are other possibilities?
What would happen if . . . ?
Can you describe an approach (strategy) you can use to solve this?
What do you need to do next?
Do you see any patterns or relationships that will help you solve this?
How does this relate to ...?
Can you make a prediction?
Why did you...?
What assumptions are you making?
Reflecting about the Solution
How do you know your solution (conclusion) is reasonable? How did you arrive at your answer?
How can you convince me your answer makes sense?
What did you try that did not work?
Has the question been answered?
Can the explanation be made clearer?
Responding (helps clarify and extend their thinking)
Tell me more.
Can you explain it in a different way?
Is there another possibility or strategy that would work?
Is there a more efficient strategy?
Help me understand this part...
Adapted from They're counting on us, California Mathematics Council, 1995
