2.2.2 Number Sentences
Understand how to interpret number sentences involving addition, subtraction and unknowns represented by letters. Use objects and number lines and create real-world situations to represent number sentences.
For example: One way to represent n + 16 = 19 is by comparing a stack of 16 connecting cubes to a stack of 19 connecting cubes; 24 = a + b can be represented by a situation involving a birthday party attended by a total of 24 boys and girls.
Use number sentences involving addition, subtraction, and unknowns to represent given problem situations. Use number sense and properties of addition and subtraction to find values for the unknowns that make the number sentences true.
For example: How many more players are needed if a soccer team requires 11 players and so far only 6 players have arrived? This situation can be represented by the number sentence 11 - 6 = p or by the number sentence 6 + p = 11.
Overview

Standard 2.2.2 Essential Understandings
Second graders build on their previous work with operations by writing number sentences to represent a real world or mathematical situation involving addition and subtraction. In addition, they write a real world problem to represent a given number sentence.
Work with number sentences continues as second graders determine if a number sentence is true or false. For example, is 9 + 7 = 14 true or false? They are also able to write their own true number sentences and false number sentences.
Second graders build on their understanding of the equal sign as they continue work with variables when finding unknowns in number sentences. The unknowns in given number sentences are found in varying positions. For example, 5 + k = 14, 5 = m - 9, 14 - r = 5. Second graders understand that a variable used more than once in a given number sentence has the same value and different variables in a given number sentence may or may not have the same value. For example, in the equation r + r = 18, "r" equals 9. In the equation a + b = 18, "a" and "b" could have the same value (9) or different values (10 and 8 or 12 and 6, etc.)
All Standard Benchmarks
2.2.2.1
Understand how to interpret number sentences involving addition, subtraction and unknowns represented by letters. Use objects and number lines and create real-world situations to represent number sentences.
2.2.2.2
Use number sentences involving addition, subtraction, and unknowns to represent given problem situations. Use number sense and properties of addition and subtraction to find values for the unknowns that make the number sentences true.
2.2.2.1
Understand how to interpret number sentences involving addition, subtraction and unknowns represented by letters. Use objects and number lines and create real-world situations to represent number sentences.
2.2.2.2
Use number sentences involving addition, subtraction, and unknowns to represent given problem situations. Use number sense and properties of addition and subtraction to find values for the unknowns that make the number sentences true.
What students should know and be able to do [at a mastery level] related to these benchmarks:
- Know the equal sign means "the same as"
- Solve equations with the unknown in any position:
24 + 79 = n; n = 24 + 79
24 + n = 103; 103 = 24 + n
n + 79 = 103: 103 = n + 79
103 - 79 = n; n = 103 - 79
103 - n = 24; 24 = 103 - n
n - 79 = 24; 24 = n - 79
20 + 52 = n + 23
- Model the above types of equations using representations including manipulatives and number lines
- Create number sentences to match given story problems
- Create story problems to match given number sentences
- Determine the truth value of number sentences
- Demonstrate an understanding of the relationship between addition and subtraction
Work from previous grades that supports this new learning includes:
- Represent real-world situations involving addition/subtraction basic facts using objects and number sentences.
- Create real-world situations corresponding to number sentences.
- Determine if number sentences involving addition/subtraction are true.
- Use number sense and models to identify the missing number in an number sentence,
- Understand basic fact families (current grade level).
NCTM Standards
Represent and analyze mathematical situations and structures using algebraic symbols.
Pre-K - 2 Expectations
- Illustrate general principles and properties of operations, such as commutativity, using specific numbers;
- Use concrete, pictorial, and verbal representations to develop an understanding of invented and conventional symbolic notations.
Use mathematical models to represent and understand quantitative relationships.
Pre-K - 2 Expectations
- Model situations that involve the addition and subtraction of whole numbers, using objects, pictures, and symbols. (NCTM, 2000)
Common Core State Standards
Represent and solve problems involving addition and subtraction.
- 2.OA.1. Use addition and subtraction within 100 to solve one- and two-step word problems involving situations of adding to, taking from, putting together, taking apart, and comparing, with unknowns in all positions, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem.
Misconceptions
Student Misconceptions and Common Errors
Students may think...
- the only format for a problem is a + b = c or a - b = c, not recognizing that it can also be c = a + b or c = a - b.
- n = 90 - 13 is read: 13 minus 90 equals n. Students need constant reminders to read left to right on either side of the equal sign.
- they can ignore the presence of letters or unknowns in an equation.
- there are rules that determine which number a letter stands for. For example, e = 5 because e is the fifth letter of the alphabet or y = 4 because y was 4 in the last number sentence.
- that a letter always has one specific value.
- different letters always represent different numbers.
- an equal sign means "and the answer is." In this way, when they see an equal sign, they want to carry out the operation preceding it. They need to think of the equal sign as meaning "is the same as."
Vignette
In the Classroom
Throughout the school year, the second graders in Mr. O's class have been working on solving story problems with a variety of contexts, using bar models to represent problems, solving problems with the unknown in various positions and writing equations to match story problems.
Mr. O. knows that different structures in problems can provide differentiation for his students. Problems where the result of the operation is unknown, is the easiest type of problem to solve - and in this case - write, because children have a great deal of experience with this type of problem. The change unknown problems are harder for children to solve. Problems that have the beginning quantity unknown are the most difficult for children to solve because it's challenging to figure out where to begin.
Mr. O.: Who's ready to write some story problems? Today we're going to build on activities we've been doing all year long. I'm going to give you some equations and you're going to write story problems to match them. What is an "equation?"
Marion:It's a number sentence with an equal sign in it.
Mr. O.:Thanks, Marion. That's a good definition. Here are three equations. What does "n" represent in these number sentences?
57 - 29 = n
57 - n = 28
n - 29 = 28
Tyler: It stands for some number. We don't know what it is - that's what we have to figure out.
Mr. O.: Nice, Tyler. What do you notice about the equations on the board?
Paul: Well, they're like a fact family.
Mr. O.: Tell me more.
Paul: I already know what the "n" stands for because the answer is right there in the three number models. See, the first two problems have the total number. Then the next problem has the other two numbers, 27 and 29. So, I know all the numbers I need - 56, 27, and 29.
Mr. O: Nice connection, Paul. The point of this lesson is to write story problems that match the equations - now you have hints for solving your problems after you write them! You're still going to have to show your work and how you came up with the equations to match your story problems.
You need to choose the unit for your problem and you can choose the equation you want to work with.

Jose: Can we do all three?
Mr. O.: Sure, but I want you to work on one equation at a time. When you've finished writing the story problem, and solving it, you may work on another equation. If you're going to work on another equation, I would like you to use the same context and just change the location of the unknown.
Alaina: Can I work with LaMya?
Mr. O.:That's fine. I want you each to write different story problems. You can even choose different equations. LaMya will help you figure out how to write yours, if you have any questions.
The class gets to work. The children are used to working collaboratively and talking while they work. They know how to help each other by asking questions and not telling each other what to do. The children have solved many story problems during the year and they have experience choosing the equations that challenge them but still have an entry point so they can be successful. Mr. O. interacts with students as they work.
Mr. O.:Ahlam, what unit would you like to use in your story problem?
Ahlam: Puppies.
Mr. O.: Okay, look at the number model you chose. Read it to me.
Ahlam: 57 minus 29 equals n.
Mr. O.: Read it another way.
Ahlam: 57 take away 29 equals n.
Mr. O: Is there another way to read it?
Ahlam: 57 subtract 29 equals n.
Mr. O.: What else can we say for this symbol (points to equal sign)?
Ahlam: Same as. It means it is the same as. 57 minus 29 is the same as n.
Mr. O.: Nice. So, how is your story problem going to start?
Ahlam:There were 57 puppies.
Mr. O.: That's a good start. Since this is a subtraction problem, what kind of action are you going to use in your story?
Ahlam: Well, they could get adopted.
Mr. O.:Okay, write that down.
Ahlam wrote,"There were 57 puppies 29 found new homes."
Mr. O.:Remember your story needs a question. What question are you going to ask?
Ahlam:How many is left?
Mr. O: Will there be more than 57 puppies or fewer than 57 puppies left?
Ahlam: Less because it's a take away problem.
Mr. O.: Will there be more than 10 puppies or fewer than 10 puppies left?
Ahlam shrugs her shoulders.
Mr. O.: Make a ball park estimate.
Ahlam: Well, 57 is between 50 and 60, but closer to 60, and 29 is almost 30. So, it would be 60 take away 30.
Mr. O.: How much would that be?
Ahlam: It's like 6 take away 3 only it's about tens, so 6 tens take away 3 tens is 3 tens which is 30.
Mr. O.: So, your answer will be about 30. Is that more than 10 or less than 10?
Ahlam: It's more than 10.
Mr. O.: Right, so please write How many puppies 'are' left, because it needs to be a plural verb. Then draw a model to show how to set your solution up.
Mr. O.moves to another table.
Lisa: Mr. O., how do you spell "dolphins?
Mr. O.: Write down the sounds that you hear, and for the "f" sound use "ph."
Lisa: Okay.
Mr. O.: Which equation are you using?
Lisa: n minus 29 is 28.
Mr. O.: Good choice. What does the "n" stand for?
Lisa:That's how many dolphins there were in the beginning.
Mr. O.:So, how are you going to start your story problem?
Lisa:There were "some" dolphins by the boat.

Mr. O.: Good start. Keep working.
Miko: I'm going to write about limos.
Mr. O.: Fun - Which equation are you going to use?
Miko: 57 minus n equals 28.
Mr. O.: What does the "n" stand for?
Miko: It's some number that is being taken away.
Mr. O.:What is going to happen with your limos?
Miko: They're going to break down.
Mr. O.: That makes sense. Are there going to be more or fewer than 57 limos that break?
Miko:Less because 28 of them will still work.
Mr. O.: Will there be more than 20 or fewer than 20 that break?
Miko: I think it will be close to 30.
Mr. O.: Why?
Miko: Because I'm starting with about 60 and there are about 30 left, so that means about 30 are broken.
Mr. O.:Sounds good, keep working.
Mr. O. went back to Ahlam to check on her progress.
Mr. O.: How did you figure out your answer?
Ahlam: I used an empty number line.
Mr. O.: How did you set it up?
Ahlam: Well, I put 29 here (on the left) and 57 here (on the right). Then I started at 29 and counted up to 57. Then I added all my jumps. The answer is 28. So, there is 28 puppies left.
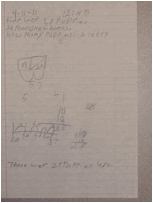
Mr. O.: There are 28 puppies left. Your work is pretty clear and I can follow what you did. Good job writing your answer in a sentence!
Lisa: Can I solve another problem now?
Mr. O.: Show me what you've done so far.

Mr. O.: Interesting. It seems like this is a subtraction problem. Why did you use addition to solve it?
Lisa: Because it's like a fact family and I know the biggest number is missing, so I have to plus the two small numbers. Adding is the opposite of minusing, and I'm missing part of my take away problem so I used adding to find it.
Mr. O.: Good thinking, Lisa. Go ahead and choose another equation to work with. Remember to still write about dolphins.
Miko: I'm finished with my story problem.
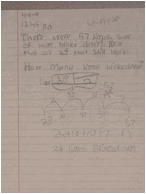
Mr. O.: It's nicely laid out, Miko. If your original equation was 57 minus n is 28, why did you write 57 minus 28?
Miko: Because I know I started with 57 limos. Some broke down, so I had 28 left. But to find out how many broke down, I had to take all the limos and take off the ones that are still working - then I can find out how many were broken. It shows it on the bar model - I'm missing a part so I can subtract the part I know.
Mr. O.: How did you figure out the answer?
Miko: I used an empty number line to add up.
Mr. O.: That's a clear explanation. Thanks, Miko.
Lisa, how is your second problem coming?
Lisa: I'm done.

Lisa:I used dolphins again.
Mr. O.: I notice that your number model matches the structure of your story problem. Then you solved it in a way that follows your number model. Nice work, Lisa!
Class, let's come back together and share some of our story problems before our time is up.
Mr. O. had several students share their story problems, with other students coming up to the board to write the matching number models, to make sure the children can go both ways - writing equations to match situations and devising situations to match equations.
Resources
Teacher Notes
- Students may need support in further development of previously studied concepts and skills.
- Research has shown that young children can use letters to represent unknowns. The number sentence 10 - s = 6 can be read 10 minus a number equals 6.
- Students need the opportunity to solve equations with the unknown in various locations. For example: 48 - m = 39, r + 15 = 38, 58 + 39 = k
- Students need to see the equal sign as a symbol of a relationship. They need to develop a broader algebraic understanding in which the expression on the left-hand side of the equals sign represents the same quantity as the expression on the right-hand side of the equals sign. They need to think of the equals sign as meaning "is the same as" instead of "the answer comes next."
- It is not necessary for teachers to teach commutativity or associativity as vocabulary words, but to on build students' understanding of the properties in observing mathematical situations and recording thinking. Students should be encouraged to investigate whether specific observations and hypotheses hold true for all cases (NCTM, 2000).
- Second graders use their number sense and knowledge of the properties of addition and subtraction in solving for an unknown. In solving 7 - m = 2, ask students what subtraction fact is related to this subtraction fact. 7 - 2 = 5. Ask, "Knowing that fact, what number is the unknown in 7 - r = 2? (5) Students may use the strategy of "counting on" to solve for the unknown. In thinking about 5 + k = 8 or 8 - 5 = k, children "count on" to find how many more it takes to get to 8.
- Modeling word problems is critical as students develop an understanding of operations and the relationships that exist between and among those operations. The bar model is an effective tool that can be used to represent the relationships in a variety of problem solving situations.
- Good questions, and good listening, will help children make sense of the mathematics, build self-confidence and encourage mathematical thinking and communication. A good question opens up a problem and supports different ways of thinking about it. The best questions are those that cannot be answered with a "yes" or a "no."
Getting Started
What do you need to find out?
What do you know now? How can you get the information? Where can you begin?
What terms do you understand/not understand?
What similar problems have you solved that would help?
While Working
How can you organize the information?
Can you make a drawing (model) to explain your thinking? What are other possibilities?
What would happen if...?
Can you describe an approach (strategy) you can use to solve this?
What do you need to do next?
Do you see any patterns or relationships that will help you solve this?
How does this relate to...?
Why did you...?
What assumptions are you making?
Reflecting about the Solution
How do you know your solution (conclusion) is reasonable? How did you arrive at your answer?
How can you convince me your answer makes sense?
What did you try that did not work? Has the question been answered?
Can the explanation be made clearer?
Responding (helps clarify and extend their thinking)
Tell me more.
Can you explain it in a different way?
Is there another possibility or strategy that would work?
Is there a more efficient strategy?
Help me understand this part ...
(Adapted from They're Counting on Us, California Mathematics Council, 1995)
NCTM Illuminations
Problems such as those in this activity help develop what students already know in preparation for writing equations and learning ways to solve for variables. Students use mathematical models to explore quantitative relationships. When presented with pictures of pan balances with one or more objects in each pan, they communicate relationships between the weights of the objects by comparing the balanced and unbalanced pans.
In this lesson, students have an opportunity to explore the foundations for equivalence, an important step in their development of algebraic thinking as they see how quantities relate. Students explore equivalence by comparing weights of different collections of objects.
Students explore the use of variables as they solve for the weights of objects using information presented in pictures. They model situations that involve adding and subtracting whole numbers, using objects, pictures, and symbols.
This lesson encourages students to explore another model of subtraction, the balance. Students will use real and virtual balances. Students also explore recording the modeled subtraction facts in equation form.
Instructional Activities
- True or False
Asking second graders to determine if a number sentence is true or false is important as second graders develop a sense of equality. It is important to use number sentences involving addition/subtraction of familiar numbers. Number sentences such as 14 = 14 and number sentences which are false (9 + 8 = 19), challenge student thinking. It is also important for second graders to consider the following types of number sentences:
6 + 7 = 6 - 7, 9 + 7 = 7 + 4, 5 + 8 = 5 + 8, 16 = 9 + 7, 7 = 15 - 8.
The following group of number sentences might be used as second graders are asked to determine if a number sentence is true or false.
True or False?
6 + 7 = 13
7 + 6 = 13
13 = 6 + 7
6 + 7 = 14
13 = 13
13 = 7 + 7
6 + 7 = 6 + 7
6 + 7 = 7 - 6
6 + 7 = 6 + 6 + 1
Additional Instructional Resources
Greenes, C., Cavanagh, M., Dacey, L., Findell, C., & Small, M. (2001). Navigating through algebra in prekindergarten-grade 2. Reston, VA: National Council of Teachers of Mathematics.
Lubinski, C. A., and Otto, A.D. (2009). Literature and algebraic reasoning. In Algebraic Thinking, Grades K - 12: Readings from NCTM's School-Based Journals and Other Publications, 99 - 105. Reston, VA: National Council of Teachers of Mathematics.
Small, M. (2009). Good questions: Great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Van de Walle, J., Karp, K., Bay-Williams, J. (2010). Elementary and middle school mathematics: Teaching developmentally. (7th ed.) Boston, MA: Allyn & Bacon.
Van de Walle, J. & Lovin, L. (2006). Teaching student-centered mathematics grades k-3. Boston, MA: Pearson Education.
Von Rotz, L., & Burns, M. (2002). Grades k-2 lessons for algebraic thinkng. Sausalito, CA: Math Solutions Publications.
Willoughby, S. S. (1997, February). Functions from Kindergarten through Sixth Grade. Teaching Children Mathematics, 3, 314 - 18.
Unknown: The number that is not known.
"Vocabulary literally is the
key tool for thinking."
Ruby Payne
Mathematics vocabulary words describe mathematical relationships and concepts and cannot be understood by simply practicing definitions. Students need to have experiences communicating ideas using these words to explain, support, and justify their thinking.
Learning vocabulary in the mathematics classroom is contingent upon the following:
Integration: Connecting new vocabulary to prior knowledge and previously learned vocabulary. The brain seeks connections and ways to make meaning which occurs when accessing prior knowledge.
Repetition: Using the word or concept many times during the learning process and connecting the word or concept with its meaning. The role of the teacher is to provide experiences that will guarantee connections are made between mathematical concepts, relationships, and corresponding vocabulary words.
Meaningful Use: Multiple and varied opportunities to use the words in context. These opportunities occur when students explain their thinking, ask clarifying questions, write about mathematics, and think aloud when solving problems. Teachers should be constantly probing student thinking in order to determine if students are connecting mathematics concepts and relationships with appropriate mathematics vocabulary.
Strategies for vocabulary development
Students do not learn vocabulary words by memorizing and practicing definitions. The following strategies keep vocabulary visible and accessible during instruction.
Mathematics Word Bank: Each unit of study should have word banks visible during instruction. Words and corresponding definitions are added to the word bank as the need arises. Students refer to word banks when communicating mathematical ideas which leads to greater understanding and application of words in context.
Labeled pictures and charts: Diagrams that are labeled provide opportunities for students to anchor their thinking as they develop conceptual understanding and increase opportunities for student learning.
Frayer Model: The Frayer Model connects words, definitions, examples and non-examples.
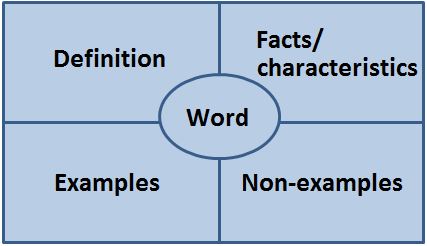
Example/Non-example Charts: This graphic organizer allows students to reason about mathematical relationships as they develop conceptual understanding of mathematics vocabulary words. Teachers should use these during the instructional process to engage student in thinking about the meaning of words.

Vocabulary Strips: Vocabulary strips give students a way to organize critical information about mathematics vocabulary words.
|
word |
definition |
illustration |
Encouraging students to verbalize thinking by drawing, talking, and writing increases opportunities to use the mathematics vocabulary words in context.
Additional Resources for Vocabulary Development
Murray, M. (2004). Teaching mathematics vocabulary in context. Portsmouth, NH: Heinemann.
Sammons, L. (2011). Building mathematical comprehension: Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
What are the key ideas related to an understanding of equality at the second grade level? How do student misconceptions interfere with mastery of these ideas?
What kind of number sentences should second graders see related to equality in an instructional setting?
Write a set of number sentences you could use with second graders in exploring their understanding of equality. Which are the most challenging for second graders?
When checking for student understanding of equality, what should teachers
- listen for in student conversations?
- look for in student work?
- ask during classroom discussions?
Examine student work related to a task involving equality. What evidence do you need to say a student is proficient? Using three pieces of student work, determine what student understanding is observed through the work.
What are the key ideas related to identifying an unknown in an equation at the second grade level? How do student misconceptions interfere with mastery of these ideas?
What kind of equations should second graders experience when identifying an unknown in an equation?
Write a set of equations you could use with second graders in exploring their understanding of identifying unknowns in equations. Which are the most challenging for second graders?
When checking for student understanding of solving for an unknown, what should teachers
- listen for in student conversations?
- look for in student work?
- ask during classroom discussions?
Examine student work related to a task involving identifying unknowns in equations. What evidence do you need to say a student is proficient? Using three pieces of student work, determine what student understanding is observed through the work.
How can teachers assess student learning related to these benchmarks?
How are these benchmarks related to other benchmarks at the second grade level?
Professional Learning Community Resources
Bamberger, H., Oberdorf, C., & Schultz-Ferrell, K.. (2010). Math misconceptions prek-grade 5: From misunderstanding to deep understanding. Portsmouth, NH: Heinemann.
Blanton, M. (2008). Algebra and the elementary classroom, transforming thinking, transforming practice. Portsmouth, NH: Heinemann.
Carpenter, T., Franke, M., & Levi, L. ( 2003). Thinking mathematically integrating arithmetic & algebra in elementary school, Portsmouth, NH: Heinemann.
Chapin, S. and Johnson, A. (2006). Math matters: Understanding the math you teach, grades k-8, 2nd edition. Sausalito, CA: Math Solutions Press.
Chapin, S., O'Connor, C., & Canavan Anderson, N. (2009). Classroom discussions: Using math talk to help students learn (Grades K-6). Sausalito, CA: Math Solutions.
Fosnot, C. T. & Jacob, B. (2010). Young mathematicians at work: Constructing algebra. Portsmouth, NH: Heinemann and Reston, VA: NCTM.
Hyde, Arthur. (2006). Comprehending math adapting reading strategies to teach mathematics, K-6. Portsmouth, NH: Heinemann.
Lester, F. (2010). Teaching and learning mathematics: Transforming research for elementary school teachers. Reston, VA: National Council of Teachers of Mathematics.
Sammons, L., (2011). Building mathematical comprehension: Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
Bamberger, H., Oberdorf, C., & Schultz-Ferrell, K. (2010). Math misconceptions prek-grade 5: From misunderstanding to deep understanding. Portsmouth, NH: Heinemann.
Bender, W. (2009). Differentiating math instruction: Strategies that work for k-8 classrooms! Thousand Oaks, CA.: Corwin Press.
Bresser, R., Melanese, K., & Sphar, C. (2008). Supporting English language learners in math class, grades k-2. Sausalito, CA: Math Solutions Publications.
Burns, Marilyn. (2007). About teaching mathematics: A k-8 resource (3rd ed.). Sausalito, CA: Math Solutions Publications.
Burns, M. (Ed). (1998). Leading the way: Principals and superintendents look at math instruction. Sausalito, CA: Math Solutions.
Caldera, C. (2005). Houghton Mifflin math and English language learners. Boston, MA: Houghton Mifflin Company.
Carpenter, T., Fennema, E., Franke, M., Levi, L., & Empson, S. (1999). Children's mathematics cognitively guided instruction. Portsmouth, NH: Heinemann.
Cavanagh, M. (2006). Math to learn: A mathematics handbook. Wilmington, MA: Great Source Education Group, Inc.
Chapin, S., & Johnson, A. (2006). Math matters: Understanding the math you teach, Grades K-8. (2nd ed.). Sausalito, CA: Math Solutions Press.
Chapin, S., O'Connor, C., & Canavan Anderson, N. (2009). Classroom discussions: Using math talk to help students learn (Grades K-6). Sausalito, CA: Math Solutions.
Dacey, L., & Salemi, R. (2007). Math for all: Differentiating instruction k-2. Sausalito, CA: Math Solutions.
Donovan, S., & Bradford, J. (Eds). (2005). How students learn: Mathematics in the classroom. Washington, DC: National Academies Press.
Dougherty, B., Flores, A., Louis, E., & Sophian, C. (2010). Developing essential understanding of number & numeration pre-k-grade 2. Reston, VA: National Council of Teachers of Mathematics.
Felux, C., & Snowdy, P. (Eds.). ( 2006). The math coach field guide: Charting your course. Sausalito, CA: Math Solutions.
Fuson, K., Clements, D., & Beckmann, S. (2009). Focus in grade 2 teaching with curriculum focal points. Reston, VA: National Council of Teachers of Mathematics.
Hyde, Arthur. (2006) Comprehending math adapting reading strategies to teach mathematics, K-6. Portsmouth, NH: Heinemann.
Kilpatrick, J., & Swafford, J. (Eds). (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academies Press.
Leinwand, S. (2000). Sensible mathematics: A guide for school leaders. Portsmouth, NH: Heinemann.
Lester, F. (2010). Teaching and learning mathematics: Transforming research for elementary school teachers. Reston, VA: National Council of Teachers of Mathematics.
Murray, M. (2004). Teaching mathematics vocabulary in context. Portsmouth, NH: Heinemann.
Murray, M., & Jorgensen, J. (2007). The differentiated math classroom-A guide for teachers k-8. Portsmouth, NH: Heinemann.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: NCTM.
Parrish, S. (2010). Number talks: Helping children build mental math and computation strategies grades K-5. Sausalito. CA: Math Solutions.
Sammons, L. (2011). Building mathematical comprehension: Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
Schielack, J., Charles, R., Clements, D., Duckett, P., Fennell, F., Lewandowski, S., ... & Zbiek, R. M. (2006). Curriculum focal points for prekindergarten through grade 8 mathematics: A quest for coherence. Reston, VA: NCTM.
Seeley, C. (2009). Faster isn't smarter: Messages about math teaching and learning in the 21st century. Sausalito, CA: Math Solutions.
Small, M. (2009). Good questions: Great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Van de Walle, J., Karp, K., Bay-Williams, J. (2010). Elementary and middle school mathematics: Teaching developmentally. (7th ed.). Boston, MA: Allyn & Bacon.
Van de Walle, J. A., & Lovin, L. H. (2006). Teaching student-centered mathematics grades K-3. Boston, MA: Pearson Education.
West, L., & Staub, F. (2003). Content focused coaching: Transforming mathematics lessons. Portsmouth, NH: Heinemann.
Assessment
- 16 - 4 = m
4 + m = 16
Which number is equal to m?
A. 10
B. 12
C. 11
D. 6
Solution: B. 12
Benchmark: 2.2.2.1
- Crystal and Dominic picked 73 strawberries altogether. Crystal picked 28 strawberries. Which number sentence matches the story?
A. 73 + 28 = s
B. 28 + s = 73
C. 73 - 45 = s
D. 28 - s = 73
Solution: B. 28 + s = 73
Benchmark: 2.2.2.2
Riannon had 15 beads this morning.
Her mom gave her 24 more.
How many beads does she have in all?
Write a number sentence to represent this story problem and answer the question, "How many beads does she have in all?"
Solution: 15 + 24 = m, 39 beads
Benchmark: 2.2.2.2
- There are twenty-five students in Mrs. Eischen's class. Twelve of the students went to library. How many students did not go to the library? Write a number sentence that can represent this situation and solve it.
Solution: 25 - 12 = n, n = 13
Benchmark: 2.2.2.1
- A soccer team requires 11 players and so far only 6 players have arrived.
How many more players are needed?
Write a number sentence with a variable for the unknown. Answer the question, "How many more players are needed?"
Solution: 6 + n = 11, 5 more players are needed (n = 5)
Benchmark: 2.2.2.2
- Write a story to go with this number sentence: 42 - n = 28
Solve the number sentence for n.
Solution: Story corresponds to the given equation, n = 14.
Benchmark: 2.2.2.2
Differentiation
More practice in looking for the related addition or subtraction fact may be necessary. Write a number sentence such as 2 + n = 8. Have students show the whole (8) with colored counters, then separate (do not remove) 2 counters to make the known part. Ask, "How many counters are left to make the missing part?" (6). If the student is ready, use the markers to illustrate the relationship between 2, 6 and 8 (Fact Family). Once students understand the relationship between addition and subtraction they can work with larger numbers.
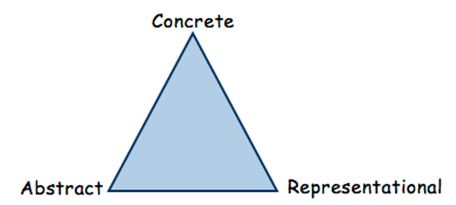
Concrete - Representational - Abstract Instructional Approach
The Concrete-Representational-Abstract Instructional Approach (CRA) is a research-based instructional strategy that has proven effective in enhancing the mathematics performance of students who struggle with mathematics.
The CRA approach is based on three stages during the learning process:
Concrete - Representational - Abstract
The Concrete Stage is the doing stage. The concrete stage is the most critical in terms of developing conceptual understanding of mathematical skills and concepts. At this stage, teachers use manipulatives to model mathematical concepts. The physical act of touching and moving manipulatives enables students to experience the mathematical concept at a concrete level. Research shows that students who use concrete materials develop more precise and comprehensive mental representations, understand and apply mathematical concepts, and are more motivated and on-task. Manipulatives must be selected based upon connections to the mathematical concept and the students' developmental level.
The Representational Stage is the drawing stage. Mathematical concepts are represented using pictures or drawings of the manipulatives previously used at the Concrete Stage. Students move to this level after they have successfully used concrete materials to demonstrate conceptual understanding and solve problems. They are moving from a concrete level of understanding toward an abstract level of understanding when drawing or using pictures to represent their thinking. Students continue exploring the mathematical concept at this level while teachers are asking questions to elicit student thinking and understanding.
The Abstract Stage is the symbolic stage. Teachers model mathematical concepts using numbers and mathematical symbols. Operation symbols are used to represent addition, subtraction, multiplication and division. Some students may not make a clean transfer to this level. They will work with some symbols and some pictures as they build abstract understanding. Moving to the abstract level too quickly causes many student errors. Practice at the abstract level will not lead to increased understanding unless students have a foundation based upon concrete and pictorial representations.
Additional Resources
Bender, W. (2009). Differentiating math instruction-Strategies that work for k-8 classrooms! Thousand Oaks, CA: Corwin Press.
Dacey, L., & Lynch, J. (2007). Math for all: Differentiating instruction grades k-2. Sausalito, CA: Math Solutions.
Murray, M. & Jorgensen, J. (2007). The differentiated math classroom-A guide for teachers k-8. Portsmouth, NH: Heinemann.
Small, M. (2009). Good questions: Great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Van de Walle, J., Karp, K., Bay-Williams, J. (2010). Elementary and middle school mathematics: Teaching developmentally. (7th ed.) Boston, MA: Allyn & Bacon.
Van de Walle, J. & Lovin, L. (2006). Teaching student-centered mathematics grades k-3. Boston, MA: Pearson Education.
English language learners find word problems much more challenging than symbolic math problems. The English language is very complex, with numerous nuances that must be learned. Students need to be able to translate common words to math symbols, natural language to algebraic expressions, and algebraic expressions to natural language. Provide extra support for ELLs as they work through the complexity of language.
Always go back to the unknown and ask, "What does the unknown represent? Have them explain what the "m" or "t" mean in a problem. A context increases the level of student understanding.
- Word banks need to be part of the student learning environment in every mathematics unit of study.
- Use vocabulary graphic organizers such as the Frayer model (see below) to emphasize vocabulary words count, first, second, third, etc.
- Sentence Frames
Math sentence frames provide support that English Language Learners need in order to fully participate in math discussions. Sentence frames provide appropriate sentence structure models, increase the likelihood of responses using content vocabulary, help students to conceptualize words and build confidence in English Language Learners.
Sample sentence frames related to these benchmarks:
|
The equation that matches the story is ________________________________. |
|
15 + m = 58 is true when m = __________. |
- When assessing the math skills of an ELL student it is important to determine if the student has difficulty with the math concept or with the language used to describe the concept and conceptual understanding.
Additional ELL Resources:
Bresser, R., Melanese, K., & Sphar, C. (2008). Supporting English language learners in math class, grades k-2. Sausalito, CA: Math Solutions Publications.
Students expand their understanding of equality by writing their own true or false number sentences on slips of paper and placing them in a container. After drawing a slip of paper from the container, students determine if the number sentence is true or false.
Students can write open number sentences on slips of paper and place them in a container. After drawing a slip of paper from the container, students tell or write a number story to match the open number sentence and then find the unknown.
Students can determine unknown numbers on magic squares.
Additional Resources
Bender, W. (2009). Differentiating math instruction-strategies that work for k-8 classrooms! Thousand Oaks, CA.: Corwin Press.
Dacey, L., & Lynch, J. (2007). Math for all: differentiating instruction grades k-2. Sausalito, CA: Math Solutions.
Murray, M. & Jorgensen, J. (2007). The differentiated math classroom-a guide for teachers k-8. Portsmouth, NH: Heinemann.
Small, M. (2009). Good questions: great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Parents/Admin
Administrative/Peer Classroom Observation
|
Students are . . . |
Teachers are . . . |
|
solving simple number sentences with the unknown represented as aletter (e.g., 15 - n =9; s + 3 = 8). |
engaging students in discussions about their strategies for solving number sentences with unknowns. |
|
justifying their solution strategies, explaining their thinking, questioning each other, forming conjectures. |
asking: Why? How do you know? Will that always work? |
|
using concrete materials to explore and describe number relationships expressed in open-ended number sentences (e.g., n + 2 = 6). |
monitoring students' use of concrete materials such as colored counters for accuracy and student understanding. |
|
using letters for unknowns to express relationships in a given problem situation. |
assessing students' use of letters for unknowns through observation and discussion. |
|
writing a number story to match a given number sentence and writing a number sentence to match a given situation. |
providing situations involving an unknown value in which the unknown is in different locations. |
What should I look for in the mathematics classroom? (Adapted from SciMathMN,1997)
What are students doing?
- Working in groups to make conjectures and solve problems.
- Solving real-world problems, not just practicing a collection of isolated skills.
- Representing mathematical ideas using concrete materials, pictures and symbols. Students know how and when to use tools such as blocks, scales, calculators, and computers.
- Communicating mathematical ideas to one another through examples, demonstrations, models, drawing, and logical arguments.
- Recognizing and connecting mathematical ideas.
- Justifying their thinking and explaining different ways to solve a problem.
What are teachers doing?
- Making student thinking the cornerstone of the learning process. This involves helping students organize, record, represent, and communicate their thinking.
- Challenging students to think deeply about problems and encouraging a variety of approaches to a solution.
- Connecting new mathematical concepts to previously learned ideas.
- Providing a safe classroom environment where ideas are freely shared, discussed and analyzed.
- Selecting appropriate activities and materials to support the learning of every student.
- Working with other teachers to make connections between disciplines to show how math is related to other subjects.
- Using assessments to uncover student thinking in order to guide instruction and assess understanding.
Additional Resources
For Mathematics Coaches
Chapin, S. and Johnson, A. (2006). Math matters: Understanding the math you teach: Grades k-8. (2nd ed.). Sausalito, CA: Math Solutions.
Donovan, S., & Bradford, J. (Eds). (2005). How students learn: Mathematics in the classroom. Washington, DC: National Academies Press.
Felux, C., & Snowdy, P. (Eds.). ( 2006). The math coach field guide: Charting your course. Sausalito, CA: Math Solutions.
Sammons, L., (2011). Building mathematical comprehension: Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
West, L., & Staub, F. (2003). Content focused coaching: Transforming mathematics lessons. Portsmouth, NH: Heinemann.
For Administrators
Burns, M. (Ed). (1998). Leading the way: Principals and superintendents look at math instruction. Sausalito, CA: Math Solutions.
Kilpatrick, J., & Swafford, J. (Eds). (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academies Press.
Leinwand, S. (2000). Sensible mathematics: A guide for school leaders. Portsmouth, NH: Heinemann.
Lester, F. (2010). Teaching and learning mathematics: Transforming research for school administrators. Reston, VA: National Council of Teachers of Mathematics.
Seeley, C. (2009). Faster isn't smarter: Messages about math teaching and learning in the 21st century. Sausalito, CA: Math Solutions.
Parent Resources
Cavanagh, M. (2004). Math to Know: A mathematics handbook. Wilmington, MA: Great Source Education Group, Inc.
Cavanagh, M. (2006). Math to learn: A mathematics handbook. Wilmington, MA: Great Source Education Group, Inc
Helping your child learn mathematics
Provides activities for children in preschool through grade 5.
What should I look for in the mathematics program in my child's school?
A Guide for Parents developed by SciMathMN.
Help Your Children Make Sense of Math
Ask the right questions
In helping children learn, one goal is to assist children in becoming critical and independent thinkers. You can help by asking questions that guide, without telling them what to do. Good questions, and good listening, will help children make sense of the mathematics, build self-confidence and encourage mathematical thinking and communication. A good question opens up a problem and supports different ways of thinking about it. The best questions are those that cannot be answered with a "yes" or a "no."
Getting Started
What do you need to find out?
What do you know now? How can you get the information? Where can you begin?
What terms do you understand/not understand?
What similar problems have you solved that would help?
While Working
How can you organize the information?
Can you make a drawing (model) to explain your thinking? What are other possibilities?
What would happen if . . . ?
Can you describe an approach (strategy) you can use to solve this?
What do you need to do next?
Do you see any patterns or relationships that will help you solve this?
How does this relate to ...?
Can you make a prediction?
Why did you...?
What assumptions are you making?
Reflecting about the Solution
How do you know your solution (conclusion) is reasonable? How did you arrive at your answer?
How can you convince me your answer makes sense?
What did you try that did not work?
Has the question been answered?
Can the explanation be made clearer?
Responding(helps clarify and extend their thinking)
Tell me more.
Can you explain it in a different way?
Is there another possibility or strategy that would work?
Is there a more efficient strategy?
Help me understand this part...
Adapted from They're counting on us, California Mathematics Council, 1995.
Algebra is a natural extension once kids have an understanding of counting, adding, and subtracting. At this level, your child is simply solving a number sentence with an unknown number. You can present your child with real-world situations and encourage them to use objects and/or write a number sentence to solve them. These are some examples:
"If I have $14 in my pocket and pay Tom and I am left with $9, how much did I pay him?" (The number sentence would be $14 - d = $9. Any letter or symbol can be used for the unknown number. Your child can use their knowledge of the related subtraction fact 14 - 9 = 5 to help them find the unknown number. Your child might show 14 dollar bills to start and remove 9 to find 5 are left. So, d=5 and I paid Tom $5).
"Summer has three pieces of gum in one pocket and five in the other. How many altogether? (3 + 5 = g, 3 + 5 = 8) If she has three in one pocket but eleven total how many in this pocket?" (11 - 3 = s or 3 + s = 11)
